In two experiments with a countinous flow calorimeter to determine the specific heat capacity of a liquid,an input power of 16 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. Find the power lost (in W) to the surrounding in each case.
The correct Answer is:8
Let power lost to surrounding be P
⇒16−P=(dmdt)s(10)and,32−P=3(dmdt)s(10)⇒32−P16−P=3⇒P=8W
Similar Questions
In an experiment of measuring specific heat of a liquid, a stream of liquid flows at a steady rate of 5gs over an electrical beater dissipating 135W and a temperature rise of 5K is observed. On increasing the rate of flow to 10gs, the same temperature rise is produced with (a) dissipation of 235W. Find the specific heat Jg−1K−1) of the liquid. (Assume heat loss to the surrounding in both the cases is same.)
View SolutionA heater supplying constant power P watts is switched on at time t=0 minutes to raise the temperature of a liquid kept in a calorimeter of negligible heat capacity. A student records the temperature of the liquid T(t) at equal time intervals. A graph is plotted with T(t) on the y-axis versus t on the x-axis. Assume that there is no heat loss to the surroundings during heating. Then,
View Solution
Knowledge Check
- Question 1 - Select One
In two experimentsb with a continous flow calorimeter to determine the specific heat capacity of a liquid, an input power of 60 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. The power lost to the surrounding in each case was-
A20 WB30 WC40 WD120 W - Question 2 - Select One
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
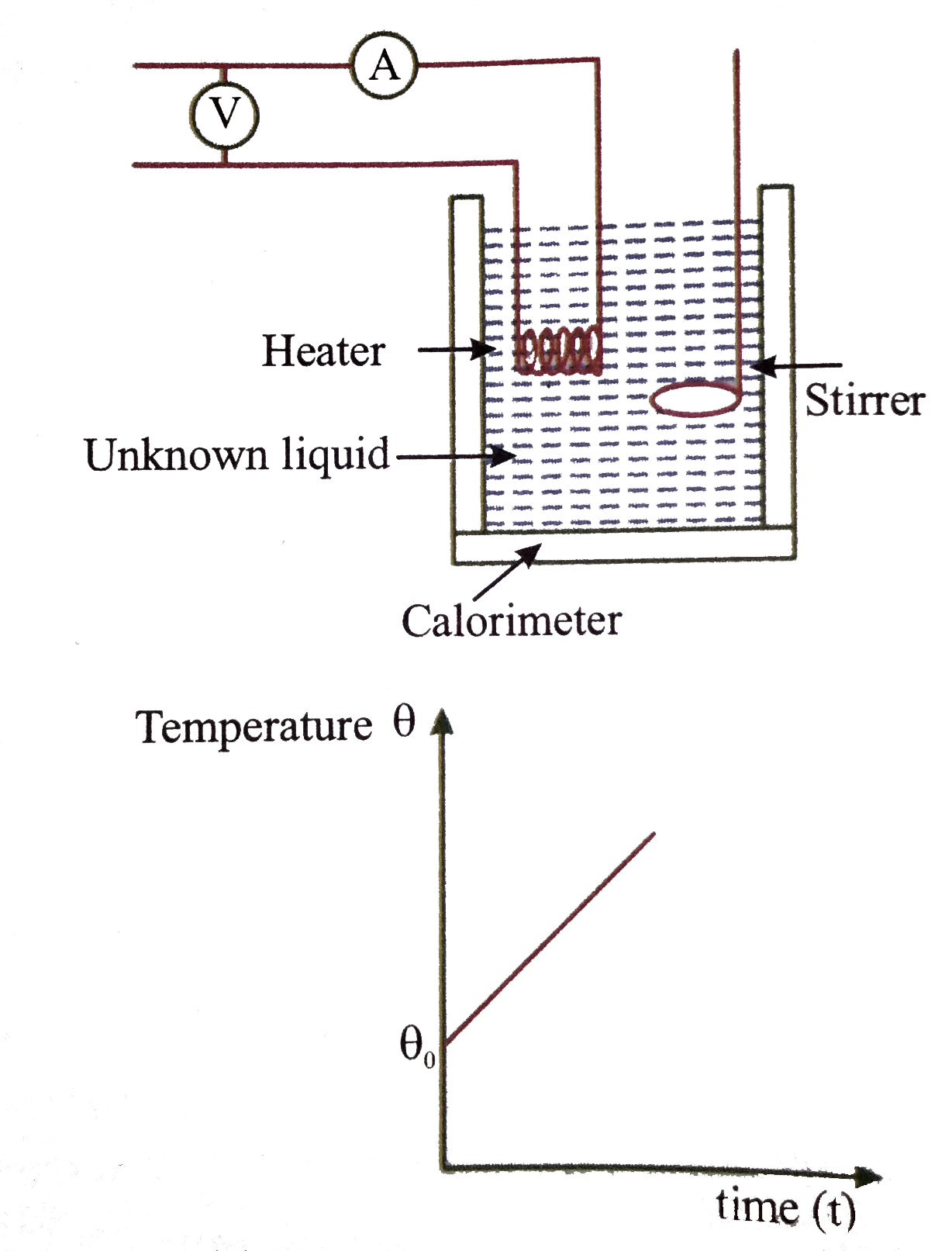
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.A3.5×103J/kg∘CB3.50×103J/kg∘CC4.0×103J/kg∘CD3.500×103J/kg∘C - Question 3 - Select One
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
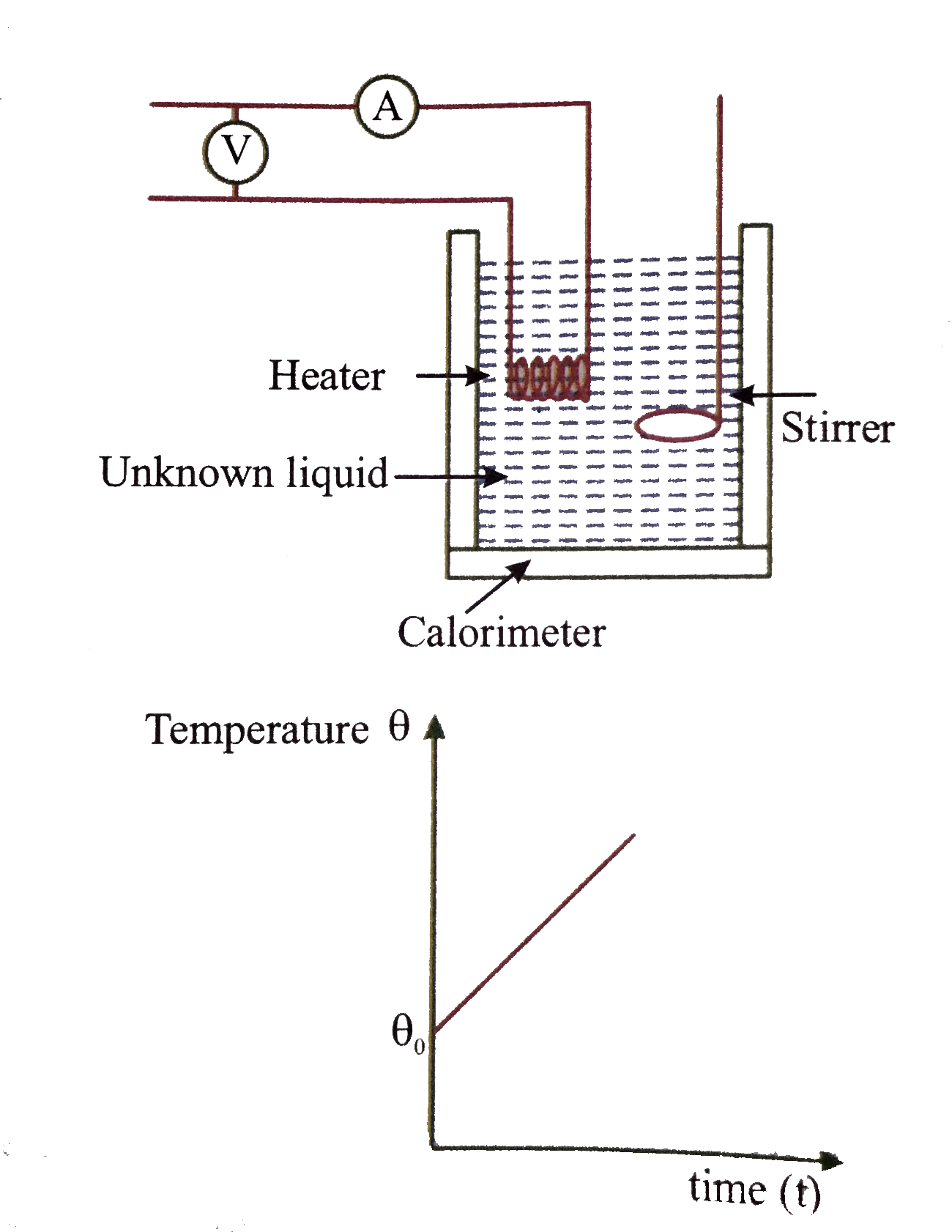
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘CA4%B5%C8%D12%
200 g of water and equal volume of another liquid of masss 250 g areplaced in turn in the same calorimeter of mass 100 g and specific heat capacity 420 J/kg K. The liquids which are constantly stirred are found to cool from 60∘C to 20∘0C in 3 minutes and 2 minutes 20 seconds, respectively. Find the specific heat capacity of the liqudi. The temperature of the surrounding is 20∘C.
View SolutionThe temperature of a hot liquid in a container of negligible heat capacity falls at the rate of 3K/min due to heat emission to the surroundings, just before it begins to solidify. The temperature then remains constant for 30min, by the time the liquid has all solidfied. Find the ratio of specific heat capacity of liquid to specific latent heat of fusion.
View SolutionA tapering glass capillary tube A of length 0.1m has diameters 10−3 m and 5×104 m at the ends. When it is just immersed in a liquid at 0∘C with larger radius in contact with liquid surface, the liquid rises 8×10−2 m in the tube. In another experiment, in a cylindrical glass capillary tube B, when immersed in the same liquid at 0∘C, the liquid rises to 6×10−2 m height. The rise of liquid in tube B is only 5.5×10−2 m when the liquid is at 50∘C. Find the rate at which the surface tension changes with temperature considering the change to be linear. The density of liquid is (1/14)×104kg/m3 and the angle of contact is zero. Effect of temperature on the density of liquid and glass is negligible.
View SolutionA cylindrical conductor has a resistance R. When the conductor is at a temperature (T) above its surrounding temperature (T0), the ratio of thermal power dissipated by the conductor to its excess temperature (ΔT=T–T0) above surrounding is a known constant k. The conductor is connected to a cell of emf V. Initially, the conductor was at room temperature T0. Mass and specific heat capacity of the conductor are m and s respectively.
(i) find the time (t) dependence of the temperature (T) of the conductor after it is connected to the cell. Assume no change in resistance due to temperature.
(ii) find the temperature of the conductor after a long time.View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
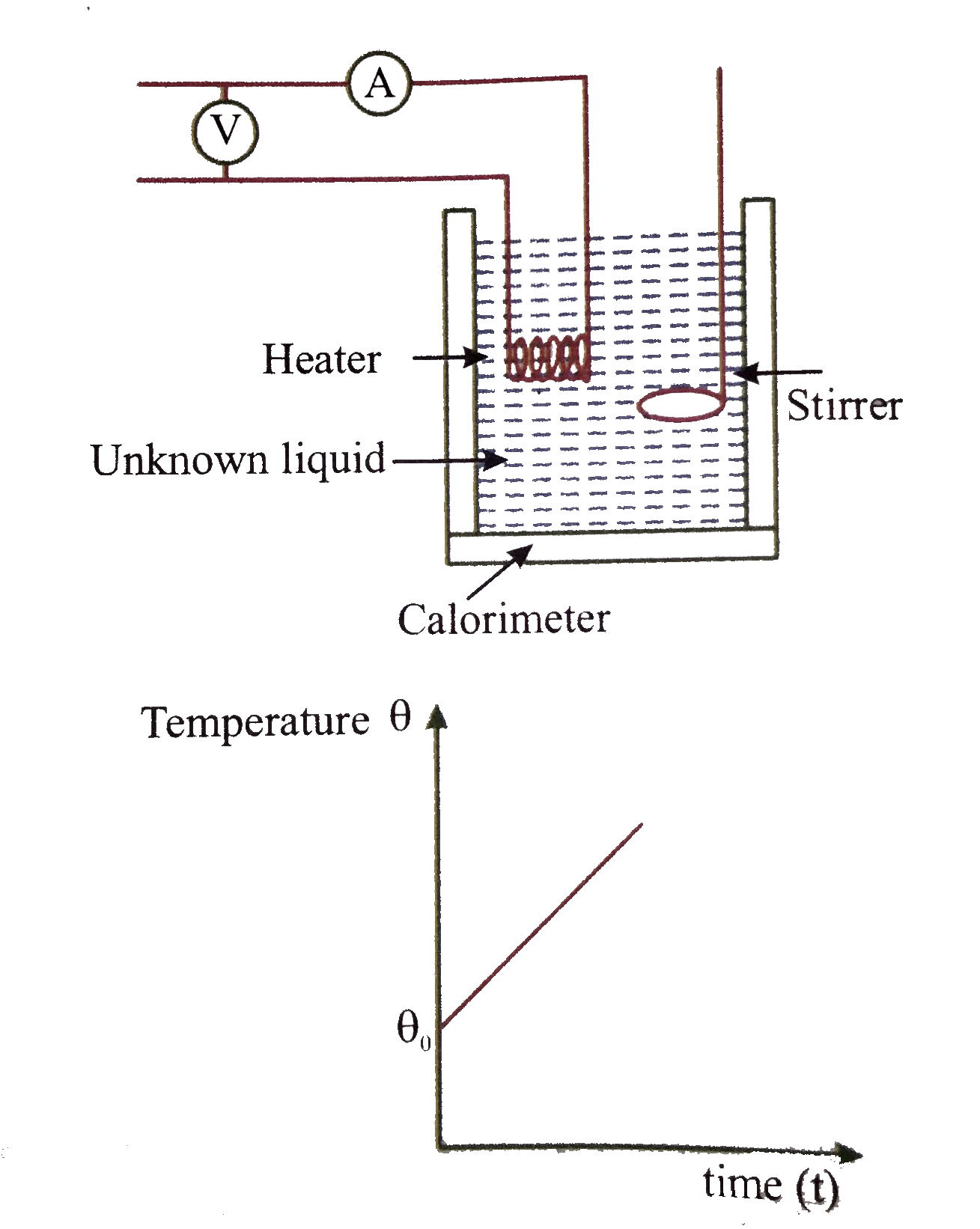
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)View Solution

