A particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as dK/dt=γt, where γ is a positive constant of appropriate dimensions. Which of the following statement is (are) true?
The force applied on the particle is constant
The speed of the particle is proportional to time
The distance of the particle from the origin increases linearly with time
The force is conservative
The correct Answer is:A, B, D
To solve the problem, we need to analyze the relationship between kinetic energy, velocity, acceleration, and the distance traveled by the particle under the influence of a force. Let's break it down step by step.
Step 1: Understanding the Change in Kinetic Energy
We are given that the rate of change of kinetic energy K with respect to time t is given by:
dKdt=γt
where γ is a positive constant.
Step 2: Finding Kinetic Energy as a Function of Time
To find the kinetic energy K as a function of time, we integrate the expression:
dK=γtdt
Integrating both sides from 0 to t:
K(t)−K(0)=∫t0γt′dt′
Since the particle is initially at rest, K(0)=0:
K(t)=γ∫t0t′dt′=γ((t′)22)t0=γt22
Step 3: Relating Kinetic Energy to Velocity
The kinetic energy K is also related to the mass m and velocity v of the particle by the formula:
K=12mv2
Setting the two expressions for kinetic energy equal gives:
12mv2=γt22
Multiplying both sides by 2:
mv2=γt2
Dividing by m:
v2=γmt2
Taking the square root:
v=√γmt
Step 4: Finding Acceleration
To find the acceleration a, we differentiate the velocity with respect to time:
a=dvdt=ddt(√γmt)=√γm
This shows that the acceleration is constant.
Step 5: Finding the Force
Using Newton's second law, the force F acting on the particle is given by:
F=ma=m⋅√γm=√γm
This indicates that the force is constant.
Step 6: Finding Distance Traveled
To find the distance x traveled by the particle, we use the relationship:
v=dxdt
Substituting for v:
dxdt=√γmt
Integrating both sides:
dx=√γmtdt
Integrating from 0 to x and 0 to t:
x=√γm∫t0t′dt′=√γm((t′)22)t0=√γm2t2
This shows that x is proportional to t2, not linearly dependent on t.
Conclusion
Based on our analysis:
1. The speed of the particle is proportional to time t (True).
2. The distance of the particle from the origin increases linearly with time (False, it increases with t2).
3. The force acting on the particle is constant (True).
4. The force is conservative (True, as it does not depend on the path).
Summary of True Statements:
- The speed of the particle is proportional to time.
- The force acting on the particle is constant.
- The force is conservative.
We are given that the rate of change of kinetic energy K with respect to time t is given by:
dKdt=γt
where γ is a positive constant.
To find the kinetic energy K as a function of time, we integrate the expression:
dK=γtdt
Integrating both sides from 0 to t:
K(t)−K(0)=∫t0γt′dt′
Since the particle is initially at rest, K(0)=0:
K(t)=γ∫t0t′dt′=γ((t′)22)t0=γt22
The kinetic energy K is also related to the mass m and velocity v of the particle by the formula:
K=12mv2
Setting the two expressions for kinetic energy equal gives:
12mv2=γt22
Multiplying both sides by 2:
mv2=γt2
Dividing by m:
v2=γmt2
Taking the square root:
v=√γmt
To find the acceleration a, we differentiate the velocity with respect to time:
a=dvdt=ddt(√γmt)=√γm
This shows that the acceleration is constant.
Using Newton's second law, the force F acting on the particle is given by:
F=ma=m⋅√γm=√γm
This indicates that the force is constant.
To find the distance x traveled by the particle, we use the relationship:
v=dxdt
Substituting for v:
dxdt=√γmt
Integrating both sides:
dx=√γmtdt
Integrating from 0 to x and 0 to t:
x=√γm∫t0t′dt′=√γm((t′)22)t0=√γm2t2
This shows that x is proportional to t2, not linearly dependent on t.
Based on our analysis:
1. The speed of the particle is proportional to time t (True).
2. The distance of the particle from the origin increases linearly with time (False, it increases with t2).
3. The force acting on the particle is constant (True).
4. The force is conservative (True, as it does not depend on the path).
- The speed of the particle is proportional to time.
- The force acting on the particle is constant.
- The force is conservative.
Similar Questions
A particle moves along the x-axis with a position given by the equation x(t) = 5 + 3t, where x is in metres, and t is in seconds. The positive directions east. Which of the following statements about the particle is false ?
View SolutionA particle of mass m is at rest at the origin at time t=0. It is subjected to a force F(t)=F0e−bt in the X - direction. Its speed V(t) is depicted by which of the following curves.

View Solution
Knowledge Check
A particle free to move along the x-axis has potential energy given as
U(x)=k[1-exp(−x2)]for −∞≤+∞, where k is a positive constant of appropriate dimensions. Then :Aat points away from origin, the particles is in equilibriumBfor any finite non-zero value of x, there is a force directed away from the originCIts total mechanical energy is k/2 and it is equal to its equal to its kinetic energy at originDat x=0, the motion of the particle is simple harmonicA particle free to move along the x-axis has potential energy given as
U(x)=k[1-exp(−x2)]for −∞≤+∞, where k is a positive constant of appropriate dimensions. Then :Aat points away from origin, the particles is in equilibriumBfor any finite non-zero value of x, there is a force directed away from the originCIts total mechanical energy is k/2 and it is equal to its equal to its kinetic energy at originDat x=0, the motion of the particle is simple harmonicA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
AAt point away from the origin, the particle is in unstable equilibriumBFor any finite non-zero value of x, there is a force directed away from the originCIf its total mechanical energy is k/2, it has its minimum kinetic energy at the originDFor small displacements from x = 0, the motion is simple harmonic
A particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
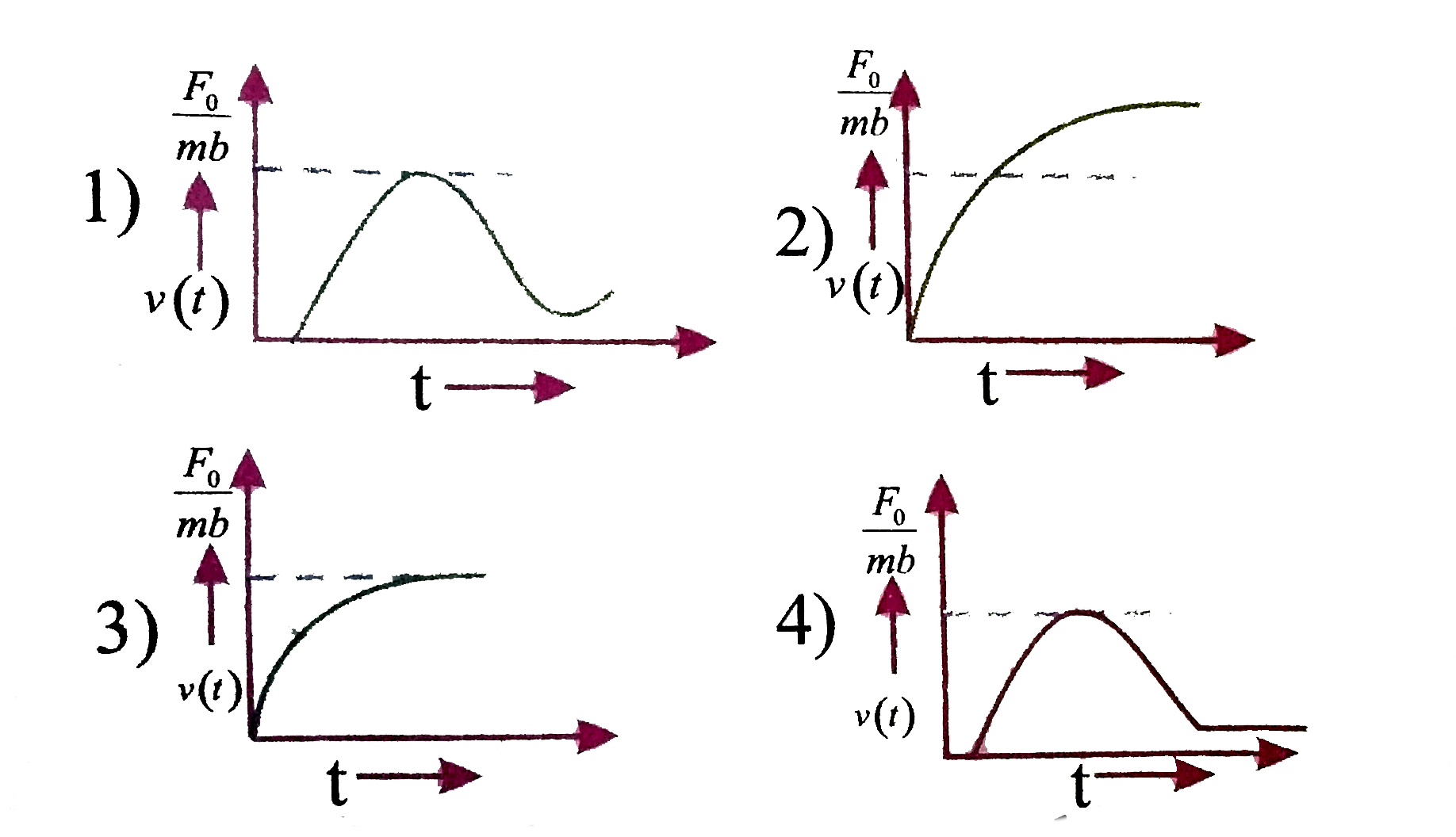
View SolutionAt time t=0s particle starts moving along the x− axis. If its kinetic energy increases uniformly with time 't', the net force acting on it must be proportional to
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionThe velocity v of a particle of mass in moving along a straight line change within time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View Solution
