Let A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
To solve the problem, we will follow these steps:
Step 1: Determine the time T taken by the particle to fall from point A to the ground.
The height from point A to the ground is h. The particle is released from rest, so its initial velocity u=0. Using the equation of motion:
s=ut+12at2
Substituting s=h, u=0, and a=g (acceleration due to gravity):
h=0⋅T+12gT2
This simplifies to:
h=12gT2
Rearranging gives:
T2=2hg
Step 2: Calculate the time TBC taken by the particle to fall from point B to point C.
The height of point B from the ground is 4h5 and the height of point C is h5. Therefore, the distance s from B to C is:
sBC=4h5−h5=3h5
Now, we need to find the velocity of the particle when it reaches point B. Using the same equation of motion:
s=ut+12at2
From A to B, the height is 4h5:
4h5=0⋅TAB+12gT2AB
This gives:
4h5=12gT2AB
Rearranging gives:
T2AB=8h5g
Now, the velocity v at point B can be calculated using:
v2=u2+2as
Here, u=0 and s=4h5:
v2=0+2g⋅4h5=8gh5
Thus, the velocity at point B is:
vB=√8gh5
Step 3: Calculate TBC.
Using the equation v=u+gt for the fall from B to C, where u=vB and v=0 at point C:
0=√8gh5−gTBC
Rearranging gives:
gTBC=√8gh5
Thus:
TBC=√8gh5g=√8h5g
Step 4: Calculate TTBC2.
Now we have:
T=√2hgandTBC=√8h5g
Calculating TTBC:
TTBC=√2hg√8h5g=√2hg⋅5g8h=√108=√54=√52
Now squaring this:
(TTBC)2=(√52)2=54
Final Result
Thus, the final answer is:
TTBC2=5
Similar Questions
A particle thrown up vertically from the ground at reaches its highest point at t=t0 =The displacement of the particle between t=7t08andt=t0 is S. Then u2Sg=
View SolutionP,Q,R and S are the points in a vertical line. It is given that PQ=QR=RS. A particle is released from rest from the point P. particle takes time tPQ,tQR and tRS to cover three equal distance, respectively. Find ratio tPQ:tQR:tRS
View Solution
Knowledge Check
Time taken by the particle to reach from A to B is t. Then the distance AB is equal to
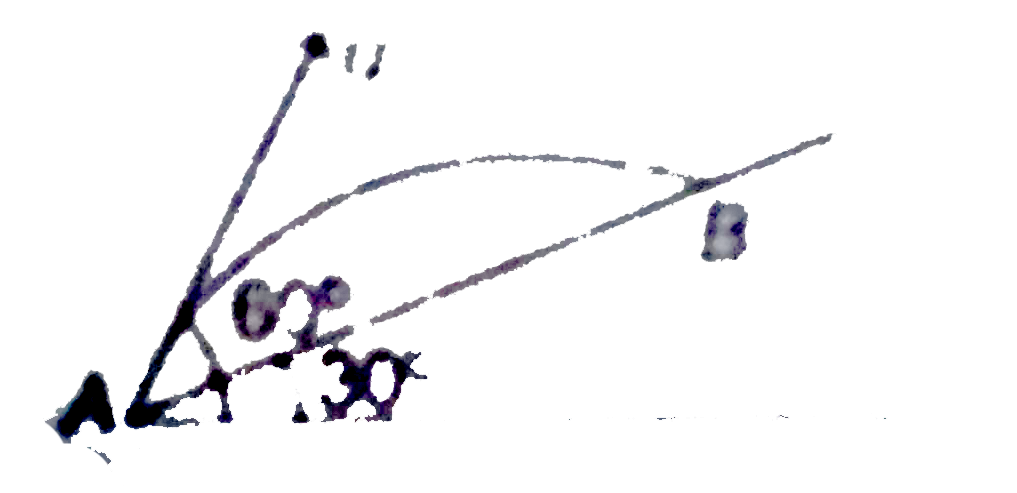 Aut√3B√3ut2C√3utD2ut
Aut√3B√3ut2C√3utD2utFor ground to ground projectile, time take by a particle to ge point O to point C is T1 and during the same motion time taken by the particle to ge from A to B is T2 then height 'h' is :
 A12gT21B14g(T21−T22)C18g(T21−T22)D18g(T2−T1)2
A12gT21B14g(T21−T22)C18g(T21−T22)D18g(T2−T1)2A particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
Ag(t−T)2BH−g(t−T)2C12g(t−T)2DH−12g(T−t)2
A paricle performs S.H.M. with time period T. The time taken by the particle to move from hall the amplitude to the maximum dispalcement is T2
View SolutionA particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t1:t2:t3 is :
View SolutionA particle is dropped from point A at a certain height from ground. It falls freely and passes through thre points B,C and D with BC=CD. The time taken by the particle to move from B to CD is 2s and from C to D is 1s. The time taken to move from A to B is s
View SolutionA particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
View SolutionA body is falling from height 'h' it takes t1 time to rech the ground. The time taken to cover the first half of height is:-
View Solution
