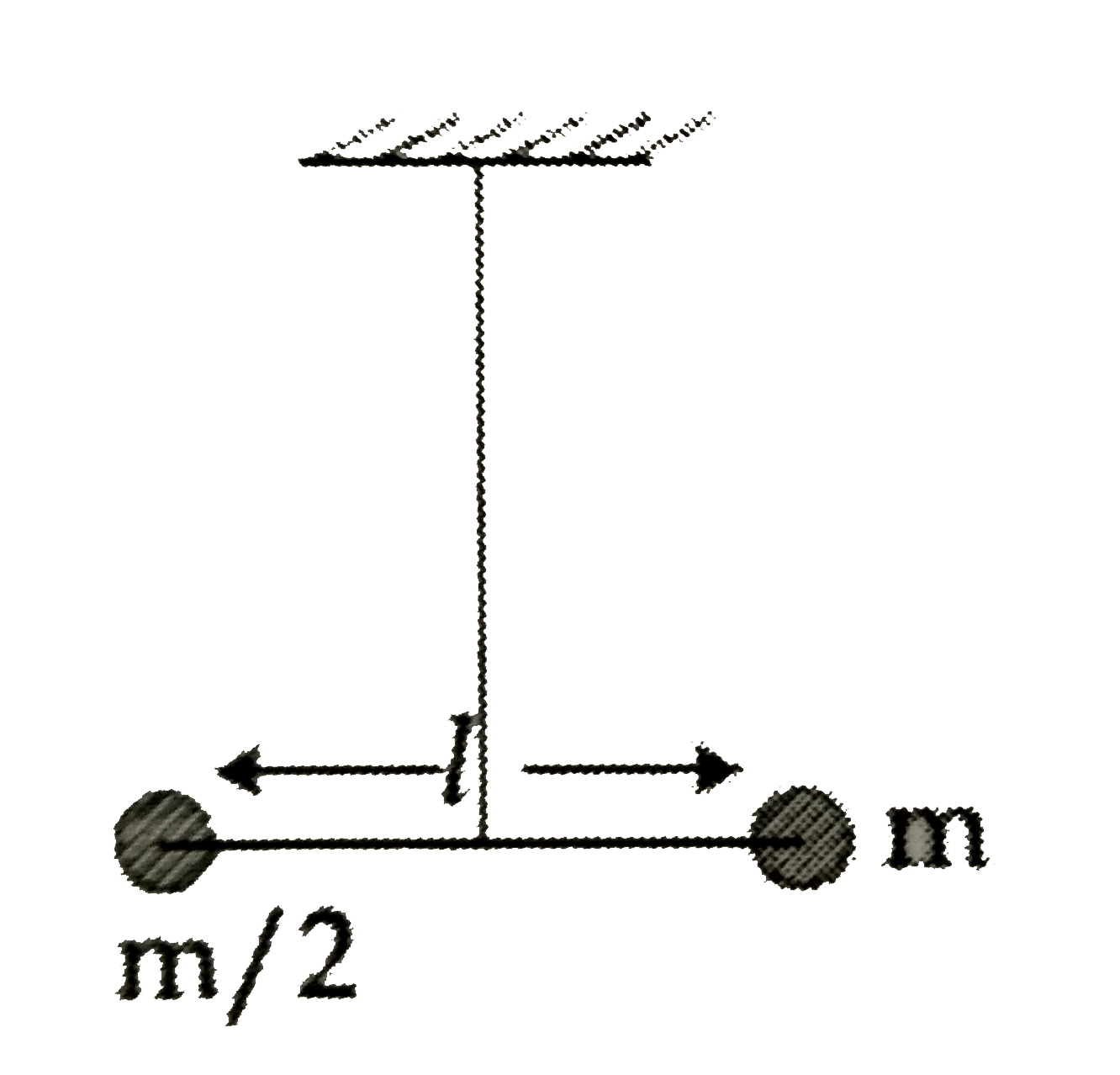
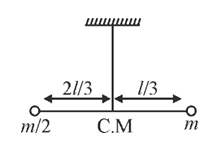
Two masses m and m2 are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is τ=kθ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be :
3kθ201
kθ2021
2kθ201
kθ201
The correct Answer is:D
Iprop=-k^(theta)
[m2(213)2+m(13)2]∝=−kθ
mI23∝=−kθ∴ω2=3kmI2
Angular velocity at mean ω0=θ0ω=θ0√3kmI2
T=mω20l3=m θ203kml2l3=kθ20l
Similar Questions
द्रव्यमान m तथा m2 के दो पिंडों को एक लम्बाई l की द्रव्यमानरहित छड़ के सिरों पर जोड़ा गया है। इस छड़ को एक मरोडांक k के तार से छड़-द्रव्यमान संयोजन के द्रव्यमान केंद्र से चित्रानुसार , लटकाया गया है। मरोडांक k के कारण छड़ के कोणीय विस्थापन θ से, उस पर बल आघूर्ण τ=kθ लगता है। यदि छड़ को θ0 कोण से घुमा कर छोड़ देते है तो , इसमें तनाव का मान , जब छड़ अपनी माध्य अवस्था से गुजरती है , होगा।
 09:51View Solution
09:51View Solutionद्रव्यमान m तथा m2 के दो पिंडों को एक लम्बाई l की द्रव्यमानरहित छड़ के सिरों पर जोड़ा गया है। इस छड़ को एक मरोडांक k के तार से छड़-द्रव्यमान संयोजन के द्रव्यमान केंद्र से चित्रानुसार , लटकाया गया है। मरोडांक k के कारण छड़ के कोणीय विस्थापन θ से, उस पर बल आघूर्ण τ=kθ लगता है। यदि छड़ को θ0 कोण से घुमा कर छोड़ देते है तो , इसमें तनाव का मान , जब छड़ अपनी माध्य अवस्था से गुजरती है , होगा।
 09:51View Solution
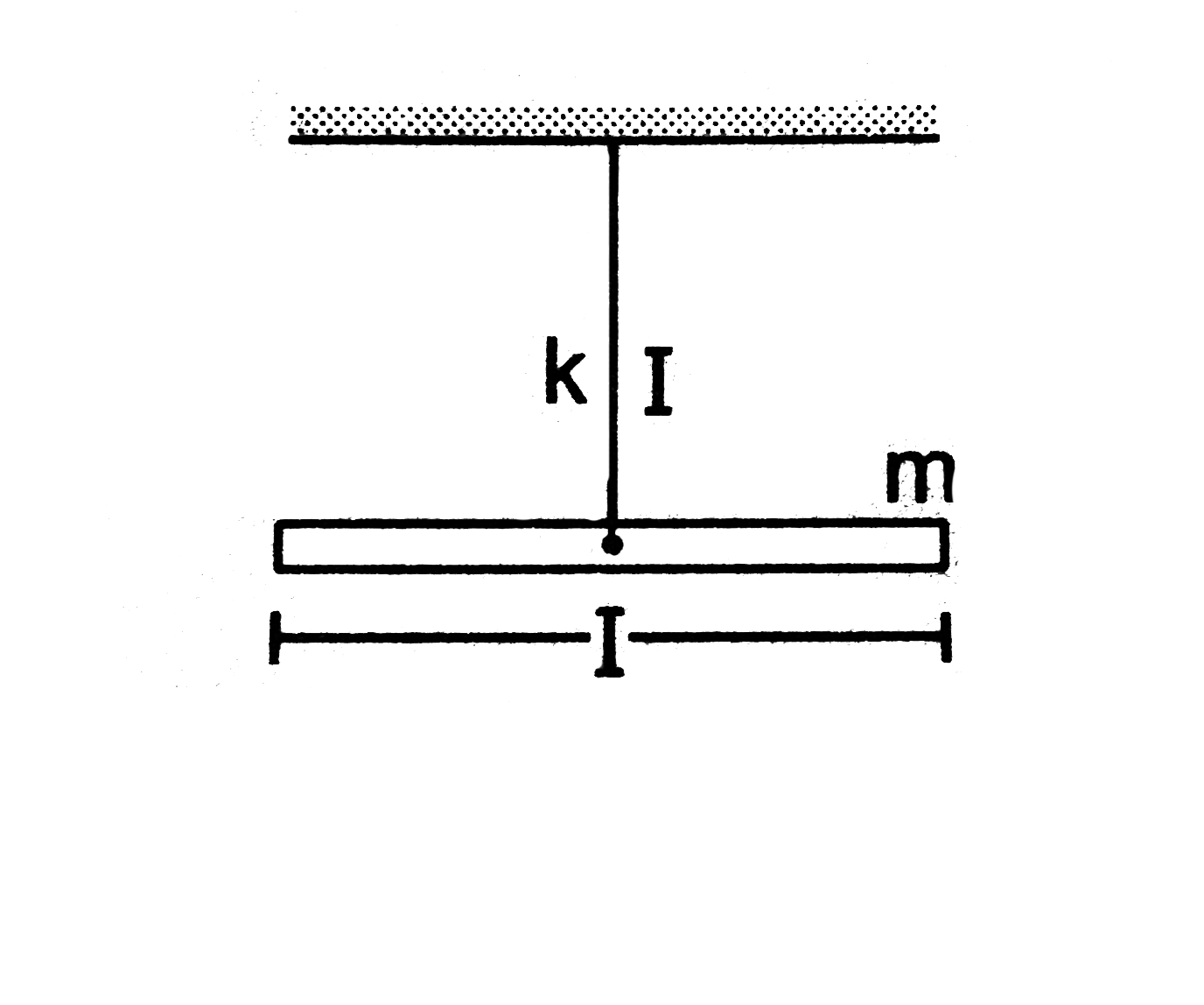
09:51View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
 01:58View Solution
01:58View SolutionTwo masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta . If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be :
09:05View SolutionFind the moment of inertia of thin and massless rod about an axis passing through its centre of mass of rod and pair of mass is suspended on both end of this rod.
02:48View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
02:33View SolutionA mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be
01:58View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
04:24View Solution
