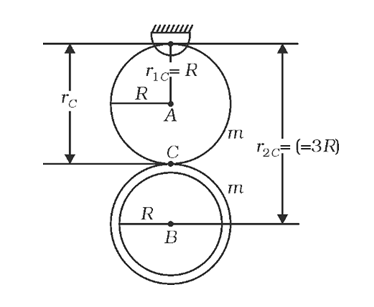
A uniform dics of mass m and radius $R = \frac{80}{23 π^{2}}$ m is pivoted smoothly at $P$ . If a uniform ring of mass $m$ and radius $R$ is welded at the lowest point of the disc, find the period of $S H M$ of the system (disc $+$ ring). (in seconds)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

Updated on:21/07/2023

For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
A uniform solid sphere of mass $m$ and radius $r$ is suspended symmetrically by a uniform thin spherical shell of radius $2 r$ and mass $m$ .
AThe gravitational field at a distance of 1.5r from the centre is $\frac{2}{9} \frac{G m}{r^{2}}$
BThe gravitational field at a distance of 2.5r from centre is $\frac{8}{25} \frac{G m}{r^{2}}$
CThe gravitational field at a distance of 1.5r from centre is zero
DThe gravitational field between the sphere and spherical shell is uniform.
The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A $\frac{1}{2} M R^{2}$
B $\frac{1}{4} M R^{2}$
C $M R^{2}$
D $\frac{3}{4} M R^{2}$