A mass hangs in equilibrium from a spring of constant K=2N/cmAnother mass of 3 kg is placed over M. Find the new amplitude of oscillation after wards (in m) (Takeg=10m/s−2)
The correct Answer is:0.15
To solve the problem step by step, we will analyze the forces acting on the mass hanging from the spring and determine the new amplitude of oscillation after adding an additional mass.
Step 1: Understand the initial equilibrium condition
When a mass M hangs from a spring with spring constant K, it stretches the spring by a distance x1 such that the force due to gravity on the mass equals the spring force.
The force due to gravity is given by:
Fg=Mg
where g=10m/s2.
The spring force is given by:
Fs=Kx1
At equilibrium:
Mg=Kx1(Equation 1)
Step 2: Introduce the additional mass
Now, when an additional mass of 3kg is placed on the original mass M, the new total mass becomes M+3kg. The new displacement from the equilibrium position becomes x2.
The new force due to gravity is:
F′g=(M+3)g
The spring force at the new displacement is:
F′s=Kx2
At the new equilibrium:
(M+3)g=Kx2(Equation 2)
Step 3: Set up the equations
From Equations 1 and 2, we have:
1. Mg=Kx1
2. (M+3)g=Kx2
Step 4: Subtract the first equation from the second
Subtract Equation 1 from Equation 2 to find the difference in displacement:
(M+3)g−Mg=Kx2−Kx1
This simplifies to:
3g=K(x2−x1)
Step 5: Solve for the amplitude
The difference x2−x1 represents the change in displacement, which is the amplitude of oscillation A:
A=x2−x1=3gK
Step 6: Substitute the values
Given:
- g=10m/s2
- K=2N/cm=200N/m (since 1cm=0.01m)
Substituting these values into the amplitude equation:
A=3×10200=30200=0.15m
Final Answer:
The new amplitude of oscillation after adding the mass is:
0.15m
When a mass M hangs from a spring with spring constant K, it stretches the spring by a distance x1 such that the force due to gravity on the mass equals the spring force.
Fg=Mg
where g=10m/s2.
Fs=Kx1
Mg=Kx1(Equation 1)
Now, when an additional mass of 3kg is placed on the original mass M, the new total mass becomes M+3kg. The new displacement from the equilibrium position becomes x2.
F′g=(M+3)g
F′s=Kx2
(M+3)g=Kx2(Equation 2)
From Equations 1 and 2, we have:
1. Mg=Kx1
2. (M+3)g=Kx2
Subtract Equation 1 from Equation 2 to find the difference in displacement:
(M+3)g−Mg=Kx2−Kx1
This simplifies to:
3g=K(x2−x1)
The difference x2−x1 represents the change in displacement, which is the amplitude of oscillation A:
A=x2−x1=3gK
Given:
- g=10m/s2
- K=2N/cm=200N/m (since 1cm=0.01m)
A=3×10200=30200=0.15m
The new amplitude of oscillation after adding the mass is:
0.15m
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionAn object of mass M oscillating with amplitude 'A' mass 'm' is added at mean position. Find new amplitude of oscillation.
View Solution
Knowledge Check
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png) A(2mghk)1/2B(k2mgh)1/2CmgkD(mgk)1/2
A(2mghk)1/2B(k2mgh)1/2CmgkD(mgk)1/2Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
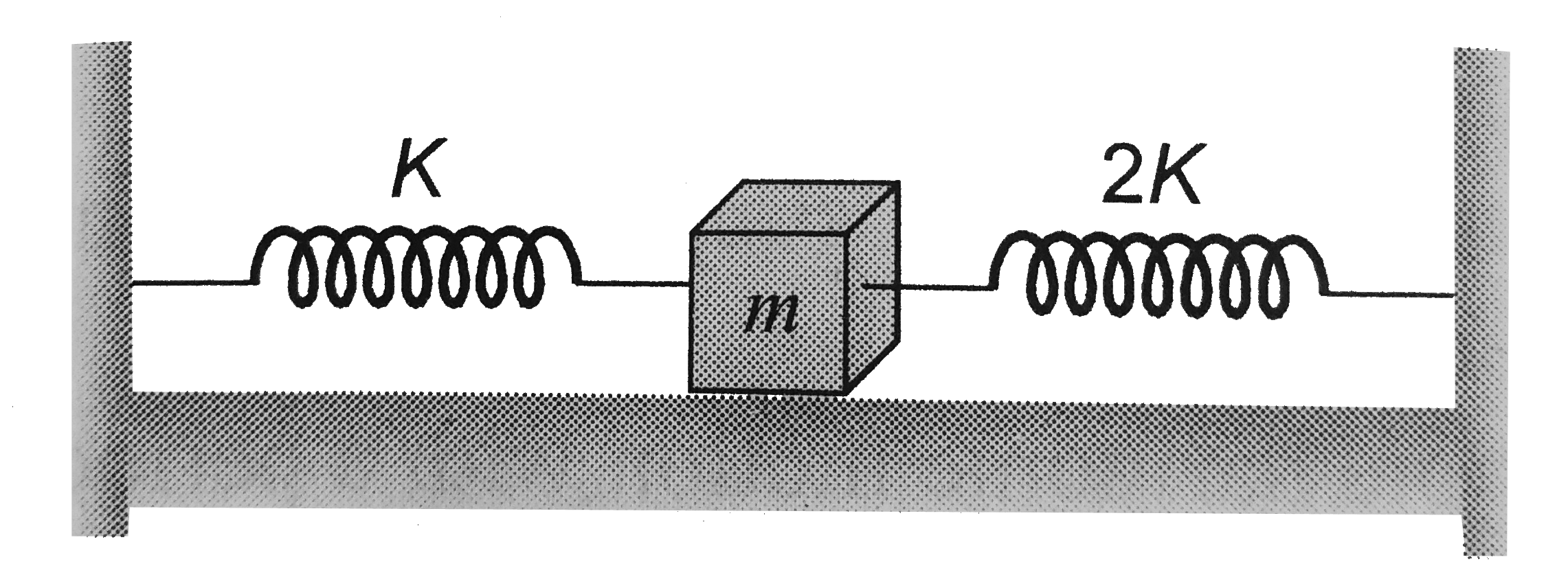 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
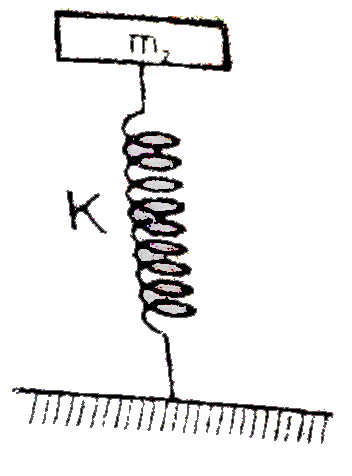
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA spring is stretched by 0.20 m , when a mass of 0.50 kg is suspended. When a mass of 0.25 kg is suspended, then its period of oscillation will be (g=10m/s2)
View SolutionNatural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
View Solution

