A mass m=100 gram is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equalt to 0.16m and time period equal to 2 second. Initially the mass is released from rest at t=0 and displacement x=−0.16 metre. The expression for the displacement of mass at any time (t) is
x=0.16cos(πt)
x=−016cos(πt)
x=0.16sin(πt+π)
x=−0.16sin(πt+π)
The correct Answer is:B
At t=0 x=-A
x=−0.16cos(πt)
Similar Questions
A mass m = 100 gm is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equal to 0.16 metre and time period equal to 2 sec. Initially the mass is released from rest at t = 0 and displacement x = –0.16 metre. The expression for the displacement of mass at any time t is
View SolutionA mass of 2 kg is attached to the spring constant 50Nm−1. The block is pulled to a distance of 5cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View Solution
Knowledge Check
A bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
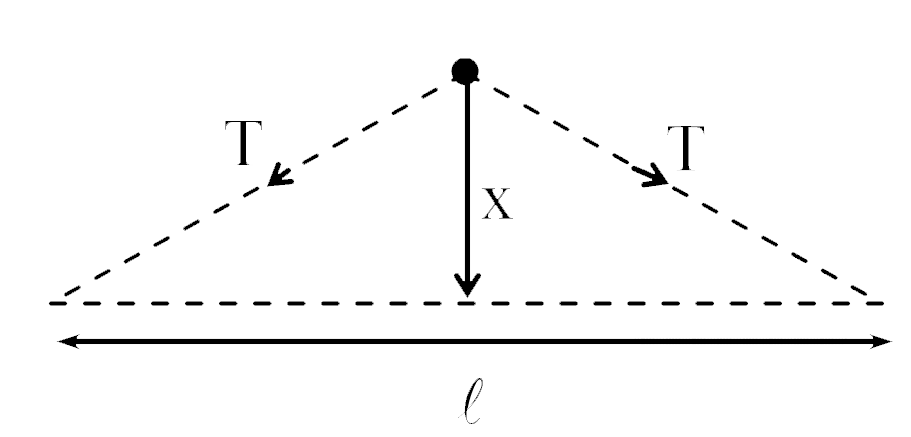
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-A12π√2TmlB12π√4TmlC12π√4TmD12π√2TmA mass m, which is attached to a spring with spring constant k, oscillates on a horizontal table, with amplitude A. At an instant when the spring is streched by √3A/2, a second mass m is dropped vertically onto the original mass and immediately sticks to it. what is the amplitude of the resulting motion-
A√32AB√78AC√1316AD√23ATwo masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
AT=2π√1k(m1m2m1+m2)BT=2π√1k(m1+m2m1m2)CT=2π√(m1k)DT=2π√(m2k)
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 seconds. If the mass of the body is increased by 4kg, Its timer period increases by 2sec. Determine value of initial mass m.
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
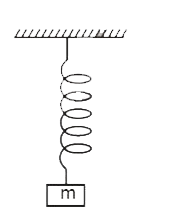
View SolutionTwo masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine value of initial mass m.
View Solution
