An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A
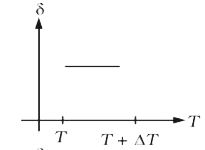
B
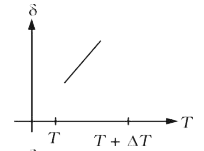
C
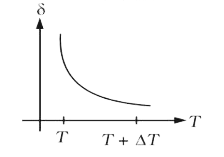
D
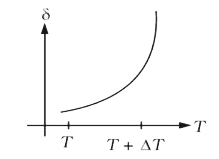
Video Solution
Text Solution
The correct Answer is:C
For an ideal gas: pV=nRT
For p = constant
pΔV=nRΔT
∴ ΔVΔT=nRp=nRnRTV=VT ∴ ΔVVΔT=1T or δ=1T
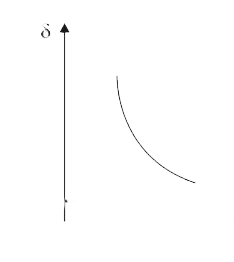
Therefore, δ is inversely proportional to temperature T. i.e.,
When T increases, δ decreases and vice-versa.
Hence, δ−T graph will be a rectangular hyperbola as shown in the above figure.
|
Similar Questions
Knowledge Check
An ideal gas is initially at temperature T and volume V. It's volume increases by ΔV due to an increase in temperature of ΔT, pressure remaining constant. The quantity μ=ΔVVΔT varies with temperature as -
A B
B C
C D
D
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A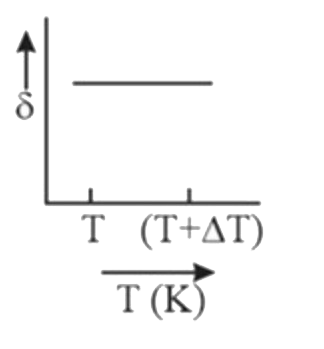 B
B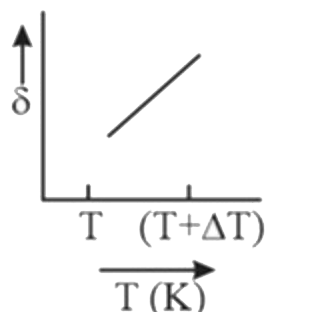 C
C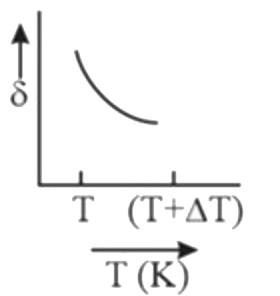 D
D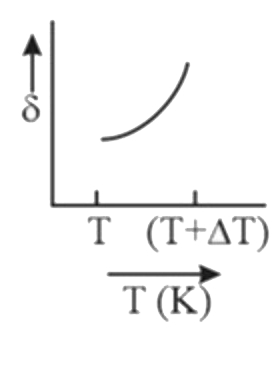
A constant temperature , the volume of a gas is to be decreased by 4 % The pressure must be increased by
A0.04B0.0416C0.08D0.0386
At constant volume, temperature is increased. Then
View SolutionThe volume of a gas is increasing adiabatically. Its temperature
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View Solution
