In the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P0 (gt atmospheric pressure Pa). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x0, then
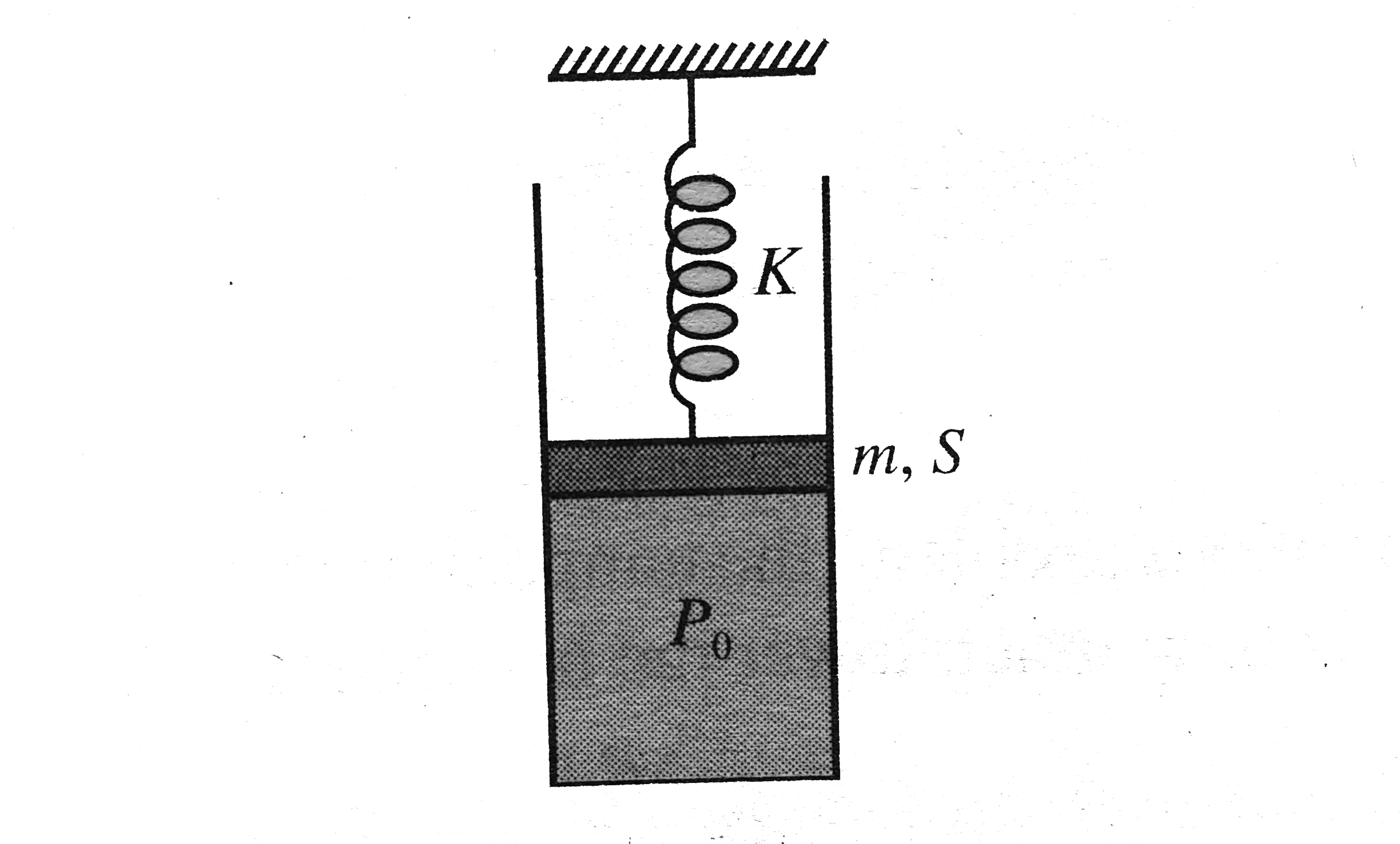
Final pressure of the gas is Pa=kx0S+mgS
Work done by gas is 12kx20+mdg0
Decrease in internal energy of gas is 2(12kx20+ m gx0+PaSx0)
Decrease in internal energy of gas is 12kx20−m gx20+PaSx0
The correct Answer is:A
Free body diagram of piston has been shown Piston is in equilibrium if PS=PaS+mg+kx0 (P=final pressure of gas ) or
P=Pa+mgS+kx0S
Work done by gas = work done against atmospheric pressure + elastic potential energy stored in the spring + increase in gravitational potential energy of the piston.
PaΔV+12kx20+mgx0
W=Pasx0+12kx20+mgx0

Since the gas in thermally insulated, work is done at the expense of internal energy of the gas. This work done is also decrease in internal energy of gas.
Hence choice C is correct and choice D is wrong.
Similar Questions
An ideal monatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monatonic gas is confined in a cylinder by a spring-loaded piston of cross section 8.0×10−3m2.initially the gas is at 300K and occupies a volume of 2.4×10−3m−3 and the sprinng is in its relaxed state. The gas is heated by a small heater until the piston moves out slowly by 0.1m. Calculate the final tenoerature of the gas. The force constant if the spring is 8000Nm−1,and the atmospheric pressure is 1.0×105Nm−2.Htecyl∈derandtheπs→narethermally∈sylated.Theπs→nandthespr∈garemass≤ssandthereisnoictionbetweentheπs→nandthecyl∈der.Neg≤ctanyheat−lossthroughthe≤adwiresoftheheater.Theheat∩acityoftheheatercoilis¬ligib≤.

View Solution
Knowledge Check
A thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then
 Afinal pressure of the gas is Kx0SBwork done by the gas is 12Kx20Cchange in internal energy of the gas is 12Kx20Dtemperature of the gas is decreased
Afinal pressure of the gas is Kx0SBwork done by the gas is 12Kx20Cchange in internal energy of the gas is 12Kx20Dtemperature of the gas is decreasedIn the cylinder shown in the figure, air is enclosed under the piston. Piston mass M=60 kg, crosssectional area of the cylinder S0=20cm2 atmospheric pressure P0=105paα=37∘. The air temperature is constant, the friction is negligible.

What is the mass of the goods that must be put on the piston so that the volume of the gas becomes half?A56kgB80kgC110 kgD92 kgA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
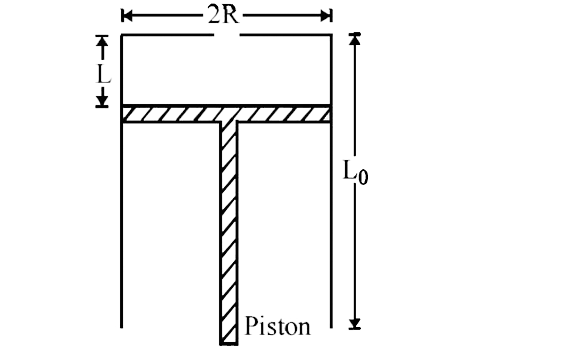
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top isA(2P0πR2πR2P0+Mg)(2L)B(P0πR2−MgπR2P0)(2L)C(P0πR2+MgπR2P0)(2L)D(P0πR2πR2P0−Mg)(2L)
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View SolutionA fixed thermally conducting cylinder has radius R and length L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
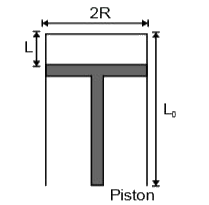
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:

View SolutionAn ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T1, pressure P1 and volume V1and the spring is in its relaxed state. The gas is tehn heated very slowly to temperature T2,pressure P2and volume V2. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View Solution
