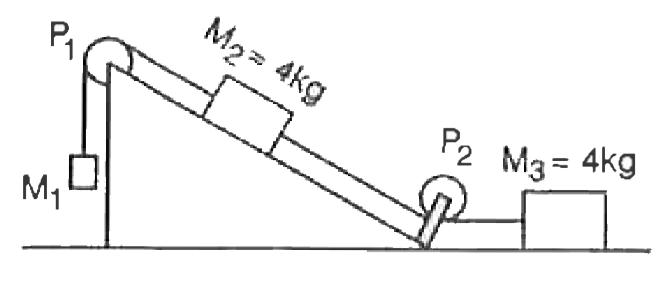
Masses $M_{1}, M_{2} and M_{3}$ are connected by string of negligible mass which pass over massless and frictionless pulleys $P_{1} and P_{2}$ as shown in figure 7.15. The masses move such that the string between $P_{1} and P_{2}$ is parallel to the incline and the portion of the string between $P_{2} and M_{3}$ is horizontal. The masses $M_{2} and M_{3}$ are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of $37^{\circ}$ with the horizontal. If the mass $M_{1}$ moves downwards with a uniform velocity, find (i) the mass of $M_{1}$ , (ii) the tension in the horizontal portion. $(g = 9.8 m s^{- 2}, {sin 37}^{\circ} = \frac{3}{5})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i) 4.2 (ii) 10

(i) The block $M_{1}$ is moving with constant speed
$m_{1} g - T = 0 \Rightarrow T - M_{1} g$

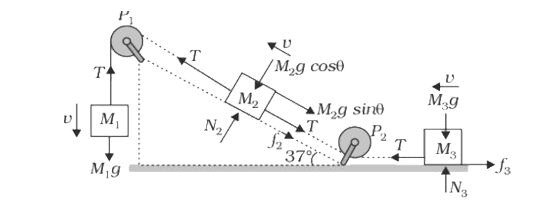
The Block $m_{1}$ is also moving with constant speed, we get
$T = T' + M_{2} g sin θ f = T' + M_{2} g sin θ + μ N_{2}$ $[∴ f_{2} = μ N_{2} = μ M_{2} g cos θ]$
(ii) $∴ T = T' + M_{2} g sin θ + μ M_{2} g cos θ$
For $M_{3}$ we get
$T' - f_{3} = M_{3} \times 0$ $\Rightarrow$ $T' = f_{3} = μ M_{3} g$
Putting the value of T and T' from (i) and (iii) in (ii) we get
$M_{1} g = μ N_{3} g + M_{2} g sin θ + μ M_{2} g cos θ$
After substituting the values, we get, $M_{1} = 4.2 k g$
The tension in the horizontal string will be
$T' = μ M_{3} g = 0.25 \times 4 \times 10 \Rightarrow T' = 10 N$

|

Updated on:21/07/2023

Class 12 PHYSICS DYNAMICS OF A PARTICLE

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between $m_{1}$ and plane is $μ$ .

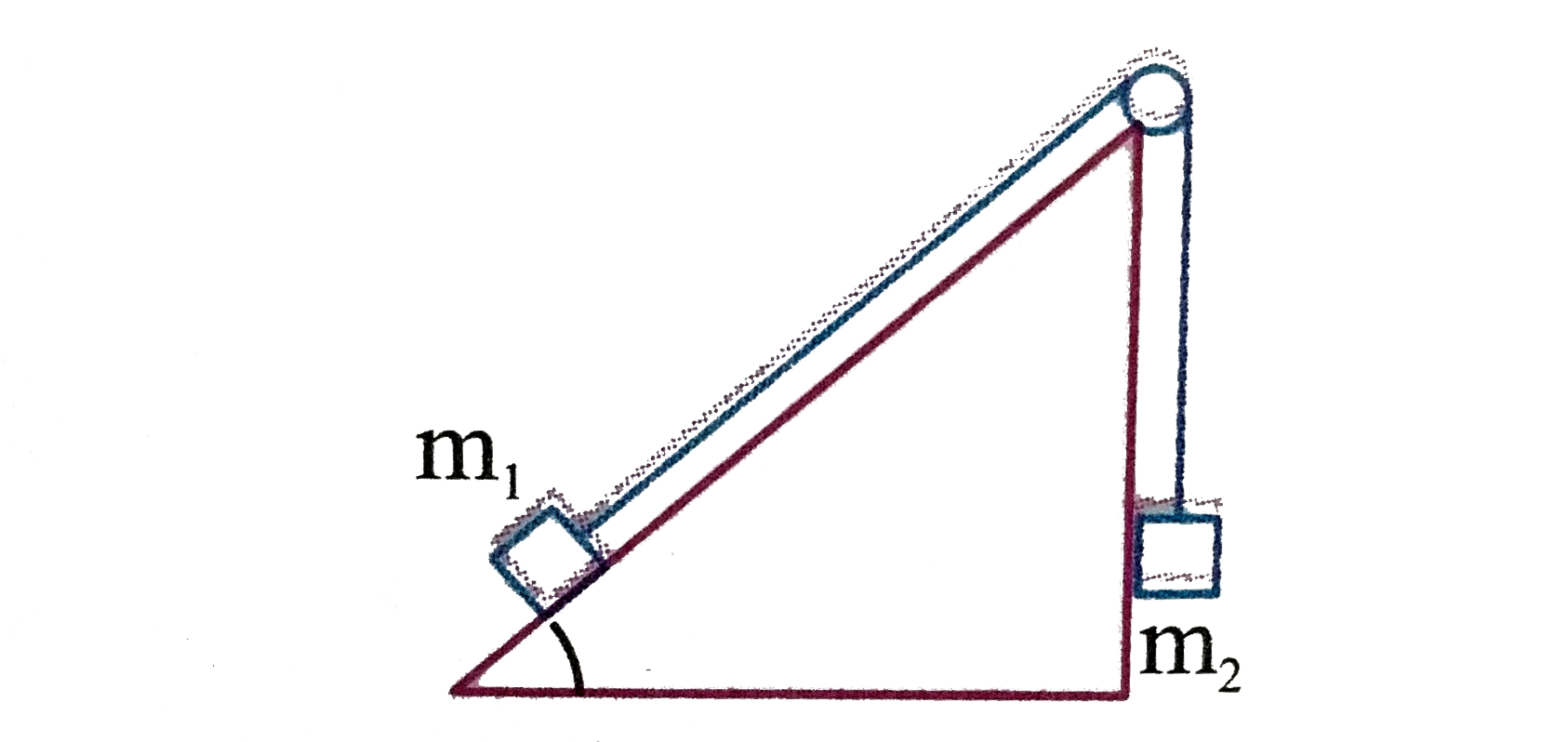AIf $m_{1} = m_{2}$ , the mass $m_{1}$ first begin to move up inclined plane when the angle of inclination $θ$ , then $μ = sec θ - tan θ$
BIf $m_{1} = m_{2}$ , then mass $m_{1}$ first begin to side down the plane if $μ = sec θ - tan θ$ .
CIf $m_{1} = 2 m_{2}$ , then mass $m_{1}$ first begins to slide down the plane if $μ = 2 tan θ$ .
DIf $m_{1} = 2 m_{2}$ , then mass $m_{1}$ first begins to slide down the plane if $μ = tan θ - \frac{1}{2} sec θ$ .
Question 2 - Select One
Blocks of mass $M_{1}$ and $M_{2}$ are connected by a cord which passes over the pulleys $P_{1}$ and $P_{2}$ as shown in the figure. If there is no friction, the acceleration of the block of mass $M_{2}$ will be

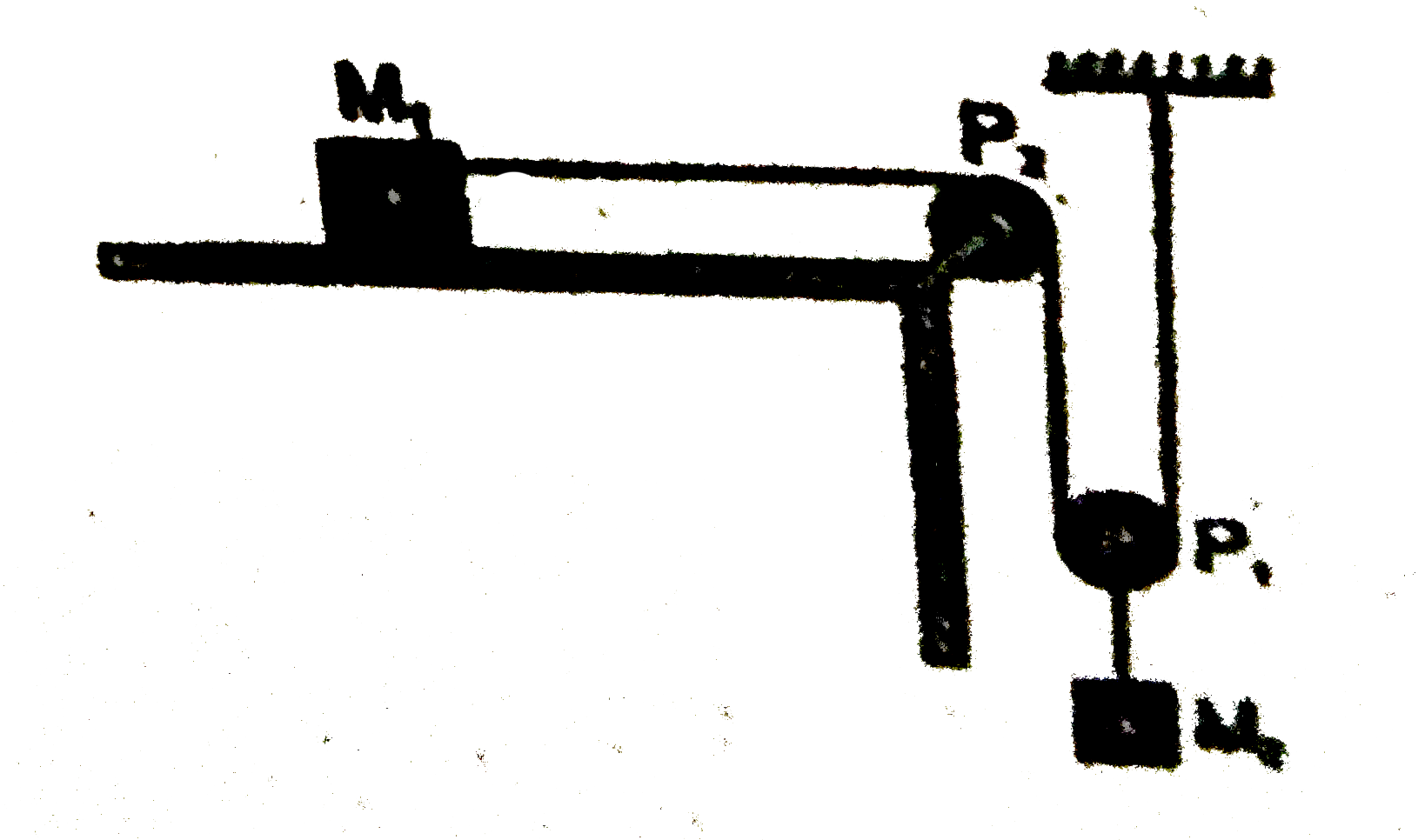A $\frac{M_{2} g}{(4 M_{1} + M_{2})}$
B $\frac{2 M_{2} g}{(4 M_{1} + M_{2})}$
C $\frac{2 M_{1} g}{(M_{1} + 4 M_{2})}$
D $\frac{2 M_{1} g}{(M_{1} + M_{2})}$
Question 3 - Select One
Two masses m and m $(m > m)$ are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A ${(\frac{m_{1} - m_{2}}{m_{1} + m_{2}})}^{2} g$
B $\frac{m_{1} - m_{2}}{m_{1} + m_{2}} g$
C $\frac{m_{1} + m_{2}}{m_{1} - m_{2}} g$
DZero

Recommended Questions

Home
Ask Doubt
Profile