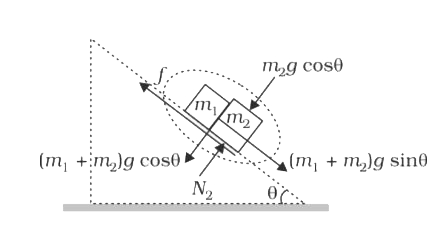
A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination θ. Various values of θ are given in List I. The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block m2 and the plane are equal to μ=0.3 . In List II expressions for the friction on block m2 are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g
[Useful information :tan(5.5∘)≈0.1,tan(11.5∘)≈0.2,tan(16.5∘)≈0.3].
![A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination theta. Various values of theta are given in List I. The coefficient of friction between the block m(1) and the plane is always zero. The coefficient of static and dynamic friction between the block m(2) and the plane are equal to mu = 0.3 . In List II expressions for the friction on block m(2) are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g [Useful information : tan (5.5^(@)) ~~ 0.1, tan (11.5^(@)) ~~ 0.2 , tan (16.5^(@))~~ 0.3].](https://d10lpgp6xz60nq.cloudfront.net/physics_images/JA_14_PHY_P2_E03_003_Q01.png)

p-1,q-1,R-1,S-3
P-2,Q-2,R-2,S-3
P-2,Q-2,R-2,S-4
P-2,Q-2,R-3,S-3
The correct Answer is:D
Condition for not sliding
fmax>(m1+m2)gsinθ
μN>(m1+m2)gsinθ
0.3m2gcosθ≥(1+2)10sinθ
6≥30tanθ
1/5≥tanθ⇒0.2≥tanθ
Now it is clear in case (P) (Q) it will not slip, friction is (m1+m2)gsinθ
⇒f=(m1+m2)gsinθ
In the case (R) (S) of they must slip so friction should be kinetic i.e. μm2gcosθ
Similar Questions
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionA block rests on a rough inclined plane making an angle of 30^@ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionTwo blocks A and B are connected by a string as shown as shown in the figure . Friction coefficient of the inclined plane is 0.5 . The mass of the block A is 5 kg. If minimum and maximum values of mass of the block B for which the block A remains in equilibrium are m_(1) and m_(2) then find the value of (m_(2) - m_(1)) [in kg]
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination theta . If coefficient of friction between the block and the inclined plane is mu , then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution
