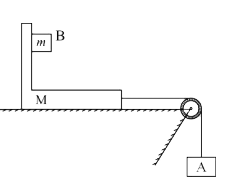
In the given situation, what is the minimum mass of block A so that block B remains stationary with respect to the wall? The coefficient of friction is μ between wall and block. All other surfaces are smooth.
(M+m)μ+1
Mμ−1
M+mμ
(M+m)μ−1
The correct Answer is:D
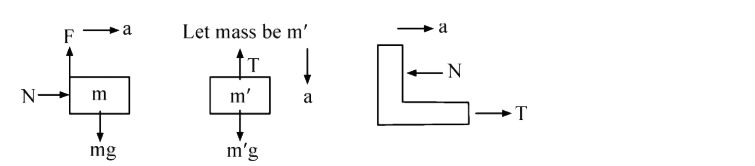
N = ma (i)
F = mg (ii)
m'g - T - m 'a (iii)
T - N = Ma (iv)
Solving (i) and (ii)
μN=mg or μma=mg ⇒a=gμ
adding (i), (iii) and (iv)
m'g=(m+m'+M)gμ ⇒m'g−m'gμ=(m+M)gμ
m(μ−1)=(m+M) ⇒m'=m+M(μ−1)
Similar Questions
Find minimum μ so that the blocks remain stationary.
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.

View Solution
Knowledge Check
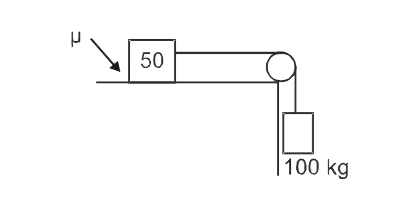
In the arrangement shown in the figure mass of the block B and A are 2m , 8m respectively. Surface between B floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that the block A remains stationary with respect to B is: (Coefficient of friction between A and B is μ and pulley is ideal).
 AmμB2mμ+1C10m1−μD10mμ−1
AmμB2mμ+1C10m1−μD10mμ−1What should be the value of F so that block of mass 1 kg remains in equilibrium. The co-efficient of friction between 1 kg and 4 kg block is 0.5 and except it all surfaces are smooth :-
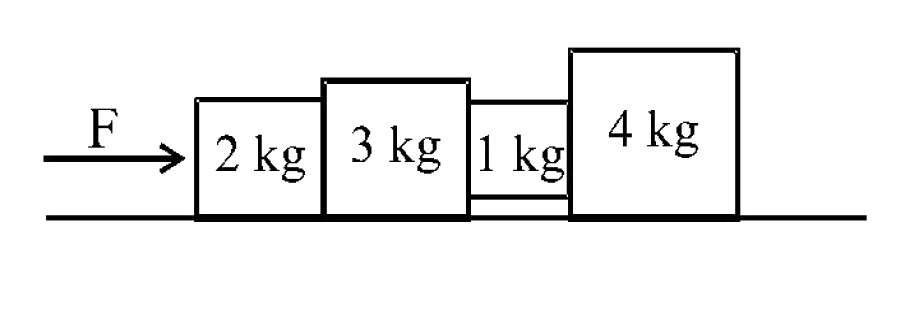 A220NB170NC135ND50N
A220NB170NC135ND50NA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
All surfaces are smooth in the adjoining figure. Find F such that block remains stationary with respect to wedge.
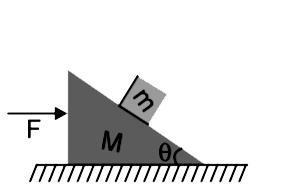
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View SolutionAll surface are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA block pressed against the vertical wall is in equilibrium. The minimum coefficient of friction is:

View Solution
