If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid?
0.25
0.18
0.3
0.4
The correct Answer is:A
v=√μRg ∴ μ=v2gR=(5)210×10=0.25
Similar Questions
Knowledge Check
A car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
A0.1B0.2C0.15D1A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
A2/5tanθB2/7tanθC5/7tanθDtanθA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AInfinitesimalBmg/4Cmg/2Dmg(1−μ)
AInfinitesimalBmg/4Cmg/2Dmg(1−μ)
What should be minimum value of F so that 2 kg slides on ground but 1kg does not slide on it? [g=10msec2]
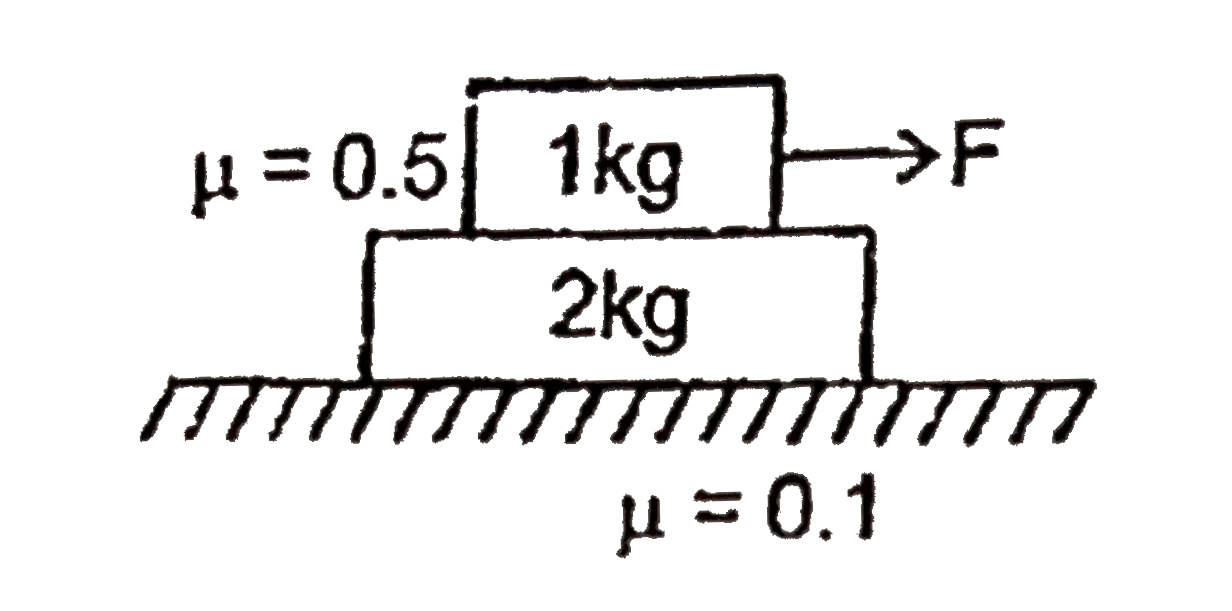
View SolutionA scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of radius 30 m. What horizontal force on the scooter is needed to make the turn possible?If the horizontal force needed for the turn in the previous problem is to be supplied by the normal force by the road what should be the proper angle of banking?
View SolutionA cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 .
.
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
View Solution
