Question

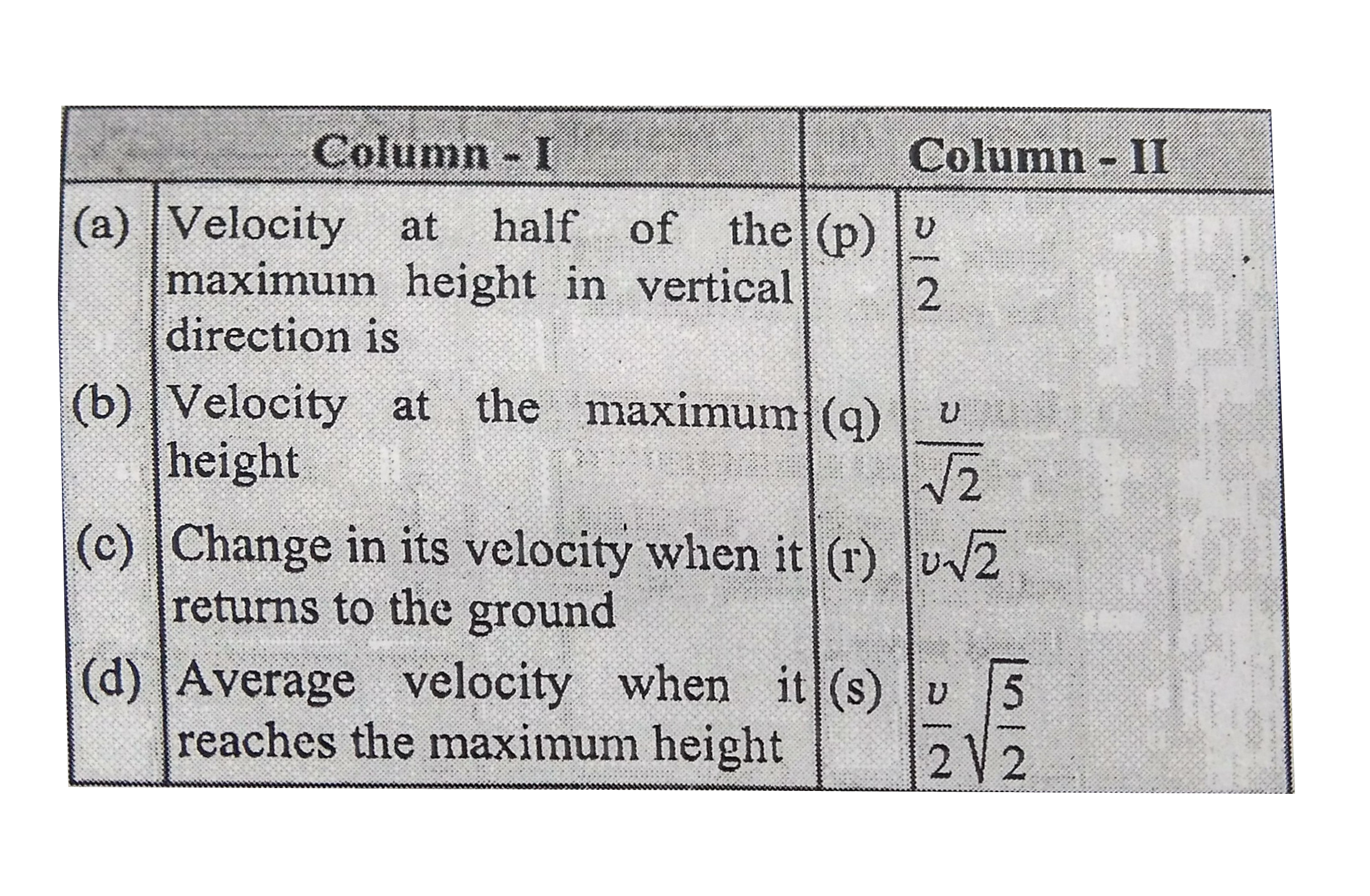
A ball is projected from the ground with velocity v such that its range is maximum. Match the columns.
COLUMN-I
(A) Velocity at half of the maximum height
(B) Velocity at the maximum height
(C) Change in its velocity when it returns to the ground
(D) Average velocity when it reaches the maximum height.
COLUMN-II
(P) $\frac{\sqrt{3}v}{2}$
(Q) $\frac{v}{\sqrt{2}}$
(R) $v\sqrt{2}$
(S) $\frac{v}{2}\sqrt{\frac{5}{2}}$

Answer

A::B::C::D

Explanation

To solve the problem, we need to match the items in COLUMN-I with those in COLUMN-II based on the physics of projectile motion. Let's break down the solution step by step.

Step 1: Understanding the Conditions for Maximum Range
The maximum range of a projectile occurs when it is launched at an angle of \(45^\circ\). For a projectile launched with an initial velocity \(v\):
- The range \(R\) is given by:
\( R = \frac{v^2 \sin(2\theta)}{g} \)
At \(\theta = 45^\circ\), \(\sin(90^\circ) = 1\), so:
\( R = \frac{v^2}{g} \)
- The maximum height \(H\) is given by:
\( H = \frac{v^2 \sin^2(\theta)}{2g} \)
At \(\theta = 45^\circ\), \(\sin^2(45^\circ) = \frac{1}{2}\), so:
\( H = \frac{v^2}{4g} \)

Step 2: Finding the Velocity at Half of the Maximum Height
At half of the maximum height (\(H/2 = \frac{v^2}{8g}\)), we can use the conservation of mechanical energy. The total mechanical energy at launch is:
\( E_{initial} = \frac{1}{2} mv^2 \)
At height \(H/2\):
\( E_{final} = \frac{1}{2} mv'^2 + mg\left(\frac{v^2}{8g}\right) \)
Setting these equal gives:
\( \frac{1}{2} mv^2 = \frac{1}{2} mv'^2 + \frac{mv^2}{8} \)
Solving for \(v'\):
\( \frac{1}{2} mv^2 - \frac{mv^2}{8} = \frac{1}{2} mv'^2 \)
\( \frac{4mv^2}{8} - \frac{mv^2}{8} = \frac{1}{2} mv'^2 \)
\( \frac{3mv^2}{8} = \frac{1}{2} mv'^2 \)
\( v'^2 = \frac{3v^2}{4} \quad \Rightarrow \quad v' = \frac{\sqrt{3}}{2} v \)
Thus, (A) matches with (P): \( \frac{\sqrt{3}v}{2} \).

Step 3: Finding the Velocity at Maximum Height
At maximum height, the vertical component of the velocity is zero, and only the horizontal component remains:
\( v_{horizontal} = v \cos(45^\circ) = \frac{v}{\sqrt{2}} \)
Thus, (B) matches with (Q): \( \frac{v}{\sqrt{2}} \).

Step 4: Change in Velocity When Returning to the Ground
The velocity vector at launch is:
\( \vec{v}_1 = \left(\frac{v}{\sqrt{2}}, \frac{v}{\sqrt{2}}\right) \)
At the ground level when it returns:
\( \vec{v}_2 = \left(\frac{v}{\sqrt{2}}, -\frac{v}{\sqrt{2}}\right) \)
The change in velocity \(\Delta \vec{v} = \vec{v}_2 - \vec{v}_1\):
\( \Delta \vec{v} = \left(0, -\frac{v}{\sqrt{2}} - \frac{v}{\sqrt{2}}\right) = \left(0, -\sqrt{2}v\right) \)
The magnitude of the change in velocity is:
\( |\Delta \vec{v}| = \sqrt{0^2 + (-\sqrt{2}v)^2} = \sqrt{2}v \)
Thus, (C) matches with (R): \( v \sqrt{2} \).

Step 5: Average Velocity When Reaching Maximum Height
The average velocity \(V_{avg}\) is given by:
\( V_{avg} = \frac{\text{Total Displacement}}{\text{Time}} \)
The displacement to the maximum height is:
\( \text{Displacement} = \left(\frac{R}{2}, H\right) = \left(\frac{v^2/g}{2}, \frac{v^2}{4g}\right) \)
The time to reach maximum height is:
\( t = \frac{v \sin(45^\circ)}{g} = \frac{v/\sqrt{2}}{g} \)
Thus,
\( V_{avg} = \frac{\left(\frac{v^2}{2g}, \frac{v^2}{4g}\right)}{\frac{v}{\sqrt{2}g}} = \left(\frac{v^2}{2g} \cdot \frac{\sqrt{2}}{v}, \frac{v^2}{4g} \cdot \frac{\sqrt{2}}{v}\right) = \left(\frac{v\sqrt{2}}{2}, \frac{v\sqrt{2}}{4}\right) \)
Calculating the average velocity gives:
\( V_{avg} = \frac{v\sqrt{2}}{2} \text{ (in terms of magnitude)} \)
This matches with (D) and (S): \( \frac{v}{2\sqrt{5/2}} \).

Final Matches:
- (A) - (P): \( \frac{\sqrt{3}v}{2} \)
- (B) - (Q): \( \frac{v}{\sqrt{2}} \)
- (C) - (R): \( v\sqrt{2} \)
- (D) - (S): \( \frac{v}{2\sqrt{5/2}} \)