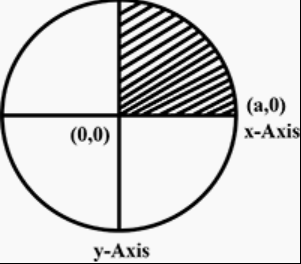
Find the area enclosed by the circle x2+y2=a2.
Given equation of circle is:
x2+y2=a2
y2=a2−x2
=> y=√a2−x2
Area of circle = 4× area of first quadrant
= 4∫a0ydx
= 4∫a0√a2−x2dx
= 4[x2√a2−x2+a22sin−1(xa)]a0
= 4[a22sin−1−0] = 2a2.π2=πa2 square unit
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.2
7 Videos
- APPLICATION OF INTEGRALSBOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - MISCELLANEOUS EXERCISE
19 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.1
18 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION
3 Videos
Similar Questions
Find the area enclosed by the circle x2+y2=25
View SolutionFind the area enclosed by the circle x2+y2=9.
View SolutionFind the area enclosed between the circle x2+y2=25 and the straight line x+y=5.
View SolutionFind the area enclosed between circle x2+y2=1 and the line x+y=1 in first quadrant.
View SolutionFind the area enclosed between the circle x2+y2=9 , along X – axis and the line x = y , lying in the first quadrant.
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the areas enclosed between the circle x2+y2−2x+4y−11=0 and the parabola y=−x2+2x+1−2√3
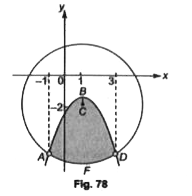
View SolutionFind the area enclosed by circle x2+y2=4 ,parabola y=x2+x+1 , the curve y=[∣∣∣sin2x4+cosx4∣∣∣] and x-axis
View SolutionFind the smaller area enclosed by the circle x2+y2=4 and the line x+y=2.
View SolutionFind the area enclosed by circle x2+y2=4, parabola y=x2+x+1, the curve y=[sin2x4+cosx4] and X-axis (where,[.] is the greatest integer function.
View Solution
