The acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
gsinθ1+12/R2
gsinθ1+I/R2
gsinθ1+I/MR2
gsinθMR2+1
The correct Answer is:C
To solve the problem of finding the acceleration down the plane of a spherical body with mass m, radius R, and moment of inertia I inclined at an angle θ to the horizontal, we can follow these steps:
Step 1: Identify the Forces Acting on the Body
The forces acting on the spherical body include:
- The gravitational force mg acting downward.
- The component of gravitational force acting down the incline, which is mgsin(θ).
- The frictional force fs acting up the incline.
Step 2: Apply Newton's Second Law for Linear Motion
According to Newton's second law, the net force acting on the body along the incline can be expressed as:
mgsin(θ)−fs=ma
where a is the acceleration of the center of mass of the spherical body.
Step 3: Apply the Torque Equation
Next, we consider the rotational motion about the center of mass. The torque τ due to the frictional force is given by:
τ=fs⋅R
This torque is also related to the angular acceleration α of the body:
τ=Iα
Since the linear acceleration a is related to angular acceleration by the equation a=Rα, we can substitute α as aR:
fs⋅R=I(aR)
From this, we can express the frictional force:
fs=IaR2
Step 4: Substitute the Frictional Force Back into the Linear Motion Equation
Now, we substitute the expression for fs back into the linear motion equation:
mgsin(θ)−IaR2=ma
Step 5: Rearrange the Equation to Solve for Acceleration a
Rearranging the equation gives:
mgsin(θ)=ma+IaR2
Factoring out a from the right side:
mgsin(θ)=a(m+IR2)
Now, we can solve for a:
a=mgsin(θ)m+IR2
Final Result
Thus, the acceleration down the plane of the spherical body is:
a=gsin(θ)1+ImR2
The forces acting on the spherical body include:
- The gravitational force mg acting downward.
- The component of gravitational force acting down the incline, which is mgsin(θ).
- The frictional force fs acting up the incline.
According to Newton's second law, the net force acting on the body along the incline can be expressed as:
mgsin(θ)−fs=ma
where a is the acceleration of the center of mass of the spherical body.
Next, we consider the rotational motion about the center of mass. The torque τ due to the frictional force is given by:
τ=fs⋅R
This torque is also related to the angular acceleration α of the body:
τ=Iα
Since the linear acceleration a is related to angular acceleration by the equation a=Rα, we can substitute α as aR:
fs⋅R=I(aR)
From this, we can express the frictional force:
fs=IaR2
Now, we substitute the expression for fs back into the linear motion equation:
mgsin(θ)−IaR2=ma
Rearranging the equation gives:
mgsin(θ)=ma+IaR2
Factoring out a from the right side:
mgsin(θ)=a(m+IR2)
Now, we can solve for a:
a=mgsin(θ)m+IR2
Thus, the acceleration down the plane of the spherical body is:
a=gsin(θ)1+ImR2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-A )
46 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )
24 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Consider a system of a small body of mass m kept on a large body of mass M placed over an inclined plane of the angle of inclination θ to the horizontal. Find the acceleration of m when the system is set in motion. Assume an inclined plane to be fixed. all the contact surfaces are smooth.

View SolutionThe pulleys in filgure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
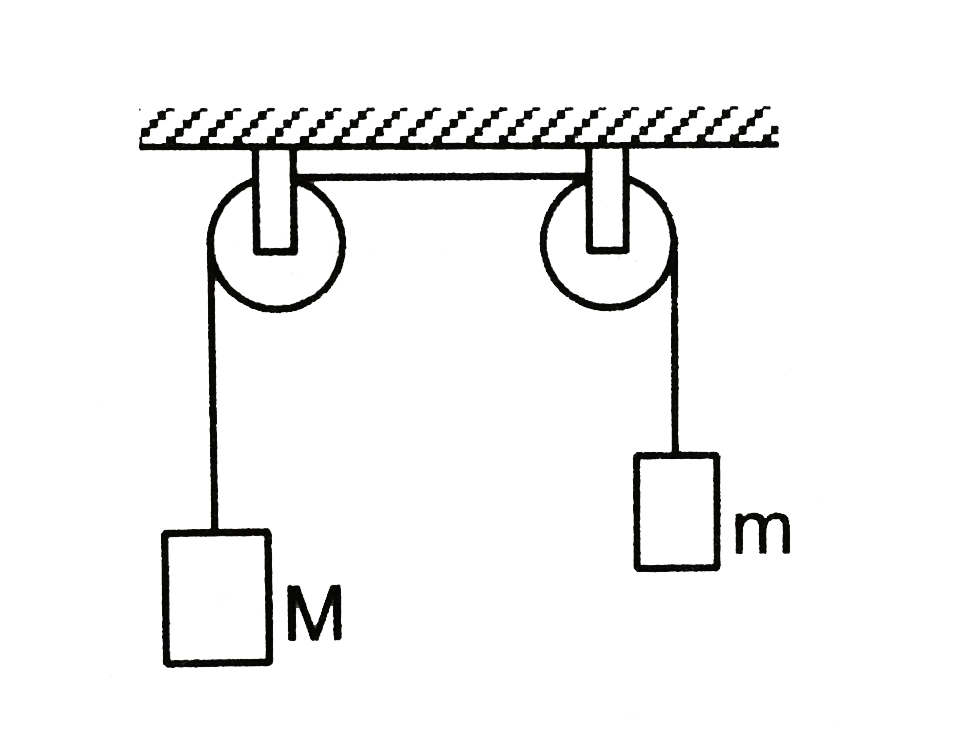
View Solution
Knowledge Check
When a body is placed on a rough plane inclined at an angle θ to the horizontal, its acceleration is
Ag(sinθ−cosθ)Bg(sinθ−μcosθ)Cg(μsinθ1−cosθ)Dgμ(sinθ−cosθ)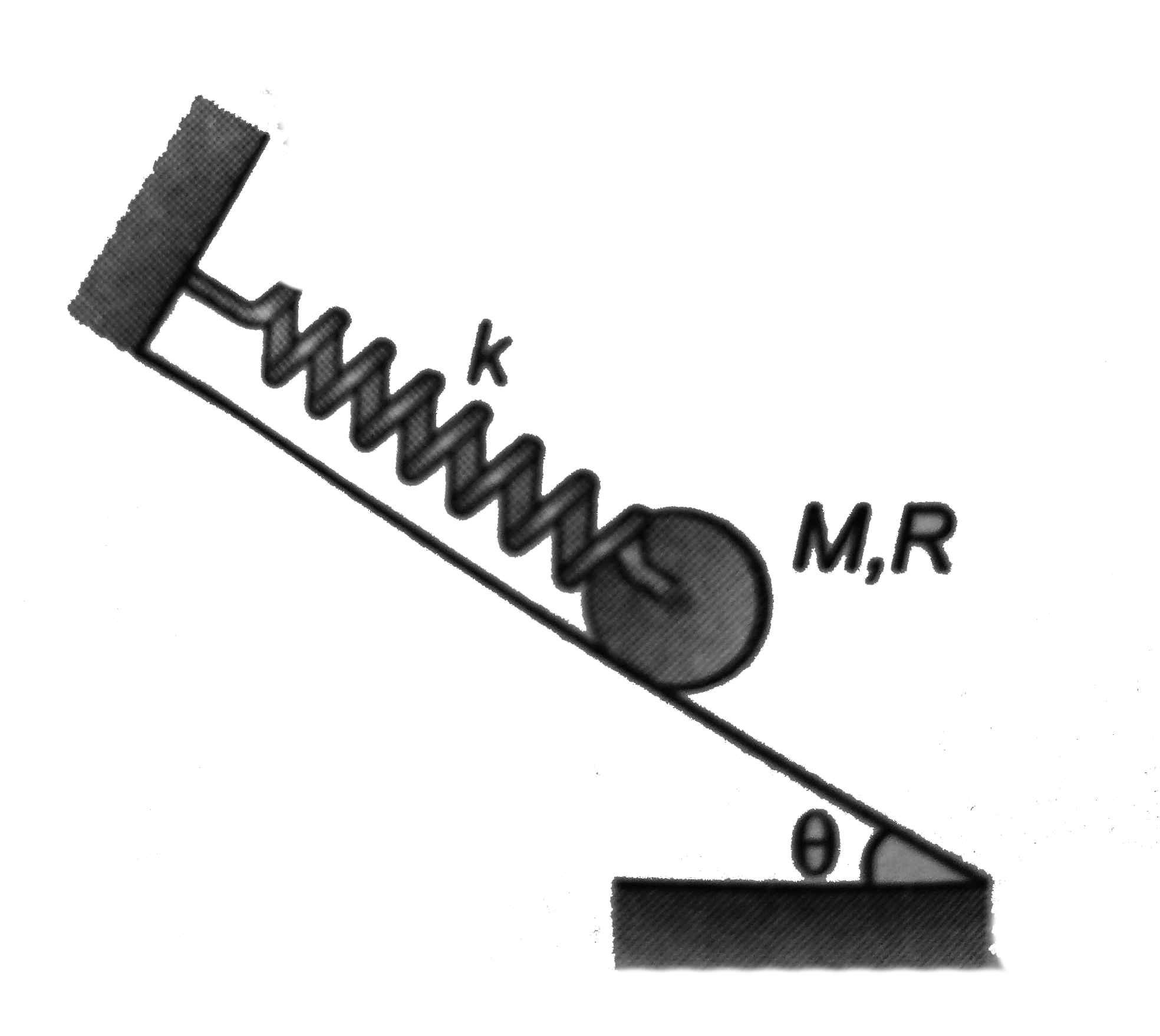
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of theseA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
Find moment of inertia of a sector of mass M , radius R and of central angle θ radians .
View SolutionA cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.

View SolutionFind moment of inertia of a sector cut from a disc of mass M, radius R and central angle θ
View SolutionA round unifrom body of radius R, mass M and moment of inertia I rolls down (without slipping) an inclined plane making an angle theta with the horizontal. Then its acceleration
View SolutionThe ratio of the accelerations for a solid sphere (mass m,andradiusR) rolling down an incline of angle θ without slipping, and slipping down the incline without rolling is
View Solution
