A cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
The phenomenon occurs in the absense of external torque, so applying law of COAM, we have
Idiscω−mvR=(Idisc+mR2)ω'⇒ω'=Iω−mvRI+mR2

Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
A disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View SolutionIn example number 12.16 suppose the disc starts rotating anticlockwise with the sae angular velocity ω=vR, then what will e the angular momentum of te disc about bottommost in this new situation?
View Solution
Knowledge Check
A cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
Alω(1+mr2)Blω+mvrl+mr2Clω−mvrl+mr2Dlω+mvrlA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchangedA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertia
The diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
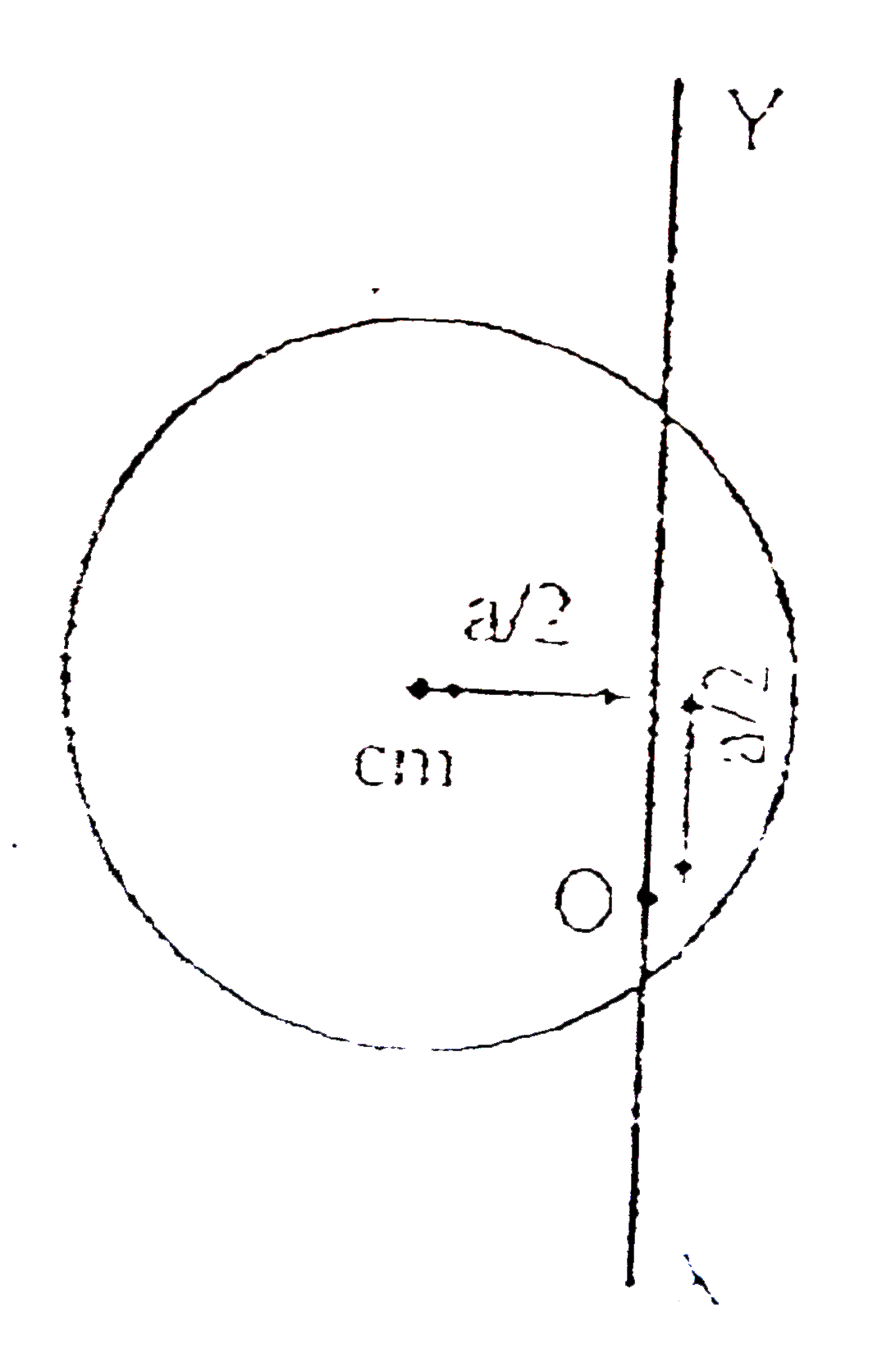
View SolutionA homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis with an angular velocity of 4 rad/s. the linear momentum of the disc is
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
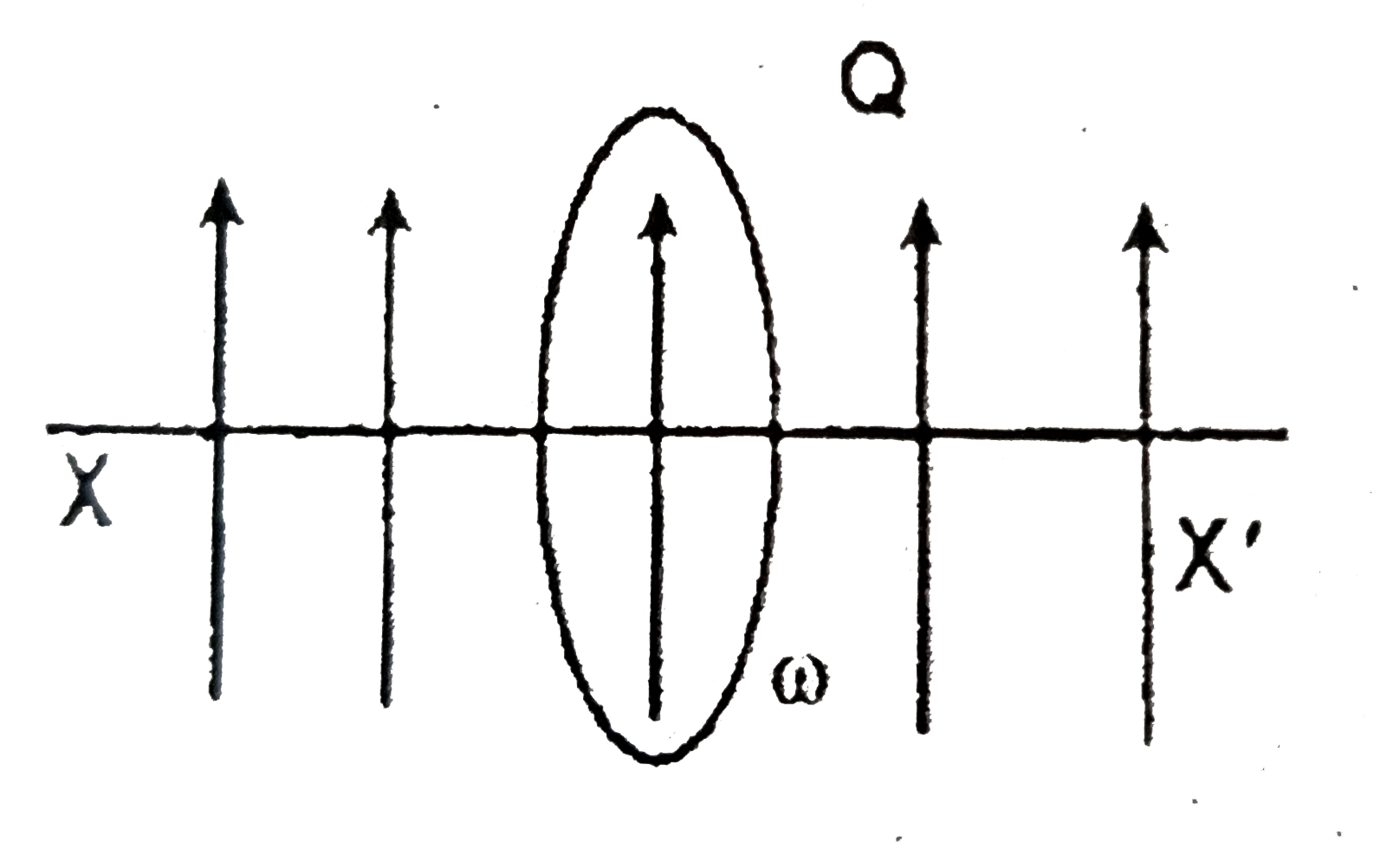
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View SolutionA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
View Solution
