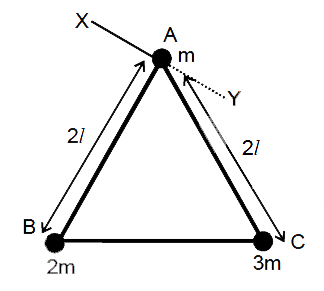
Three light rods, each of length 2l, are joined together to form a triangle. Three particles A, B, C of masses m, 2m, 3m are fixed to the vertices of the triangle. Find the moment of inertia of the resulting body about
an axis through A perpendicular to the plane ABC,
B is at a distant 2l from the axis XY so the moment of inertia of B (IB) about XY is 3m (2l)2 and IA about XY is m(0)2
Therefore the moment of inertia of the body about XY is
2m(2l)2+3m(2l)2+m(0)2=20ml2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Three light rods, each of length 2e, are joined together to form a triangle. Three particles A, B, C of masses m, 2m, 3m are fixed to the vertices of the triangle. Find the moment of inertia of the resulting body about
an axis passing through A and the midpoint of BC.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View Solution
Knowledge Check
Three particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
A3ma2Bma2Cma2/3D2/3ma2Moment of inertia of a rod of mass 'M', length ? about an axis perpendicular to it through one end is,
AMl22,BMl23CMl212DNone of these
Three particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
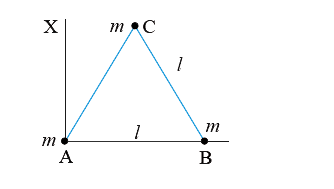
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles A,B and C of masses m,2m and 3m are placed on a straight line of length 2L as shown. Find the M.I. about an axis passing through B and perpendicular to the line AC.
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View Solution
