$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The graph of y = f (x) is best represented by

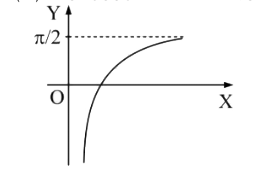
ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for f: (0,oo) to (-pi/2,pi/2)" be defined as, "f(x)=tan^(-1) (log_(e)x). The graph of y = f (x) is best represented by by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DIFFERENTIAL EQUATIONS

Knowledge Check

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The above function can be classified as :
Ainjective but not surjective
Bsurjective but not injective
Cneither injective nor surjective
Dboth injective as well as surjective
$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
If $x_{1}, x_{2} and x_{3}$ are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then $(x_{1} + x_{2} + x_{3}) is :$
A2
B3
Cgreater than 3
Dbelong to
Let $f : I - {- 1, 0, 1} \to [- π, π]$ be defined as $f (x) = 2 {tan}^{- 1} x - {tan}^{- 1} (\frac{2 x}{1 - x^{2}})$ , then which of the following statements (s) is (are) correct ?
Af(x) is bijective
Bf(x) is injective but not surjective
Cf(x) is neither injective nor surjective
Df(x) is an odd function

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The graph of y = f (x) is best represented by

The correct Answer is:C

Similar Questions

Knowledge Check

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The above function can be classified as :

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
If $x_{1}, x_{2} and x_{3}$ are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then $(x_{1} + x_{2} + x_{3}) is :$

Let $f : I - {- 1, 0, 1} \to [- π, π]$ be defined as $f (x) = 2 {tan}^{- 1} x - {tan}^{- 1} (\frac{2 x}{1 - x^{2}})$ , then which of the following statements (s) is (are) correct ?

Recommended Questions

f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex). The graph of y = f (x) is best represented by

The correct Answer is:C

Similar Questions

Knowledge Check

f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex). The above function can be classified as :

f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex). If x1,x2andx3 are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then (x1+x2+x3) is :

Let f:I−{−1,0,1}→[−π,π] be defined as f(x)=2tan−1x−tan−1(2x1−x2), then which of the following statements (s) is (are) correct ?

Recommended Questions

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The graph of y = f (x) is best represented by

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
The above function can be classified as :

$f : (0, \infty) \to (- \frac{π}{2}, \frac{π}{2}) be defined as, f (x) = {tan}^{- 1} ({log}_{e} x)$ .
If $x_{1}, x_{2} and x_{3}$ are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then $(x_{1} + x_{2} + x_{3}) is :$

Let $f : I - {- 1, 0, 1} \to [- π, π]$ be defined as $f (x) = 2 {tan}^{- 1} x - {tan}^{- 1} (\frac{2 x}{1 - x^{2}})$ , then which of the following statements (s) is (are) correct ?