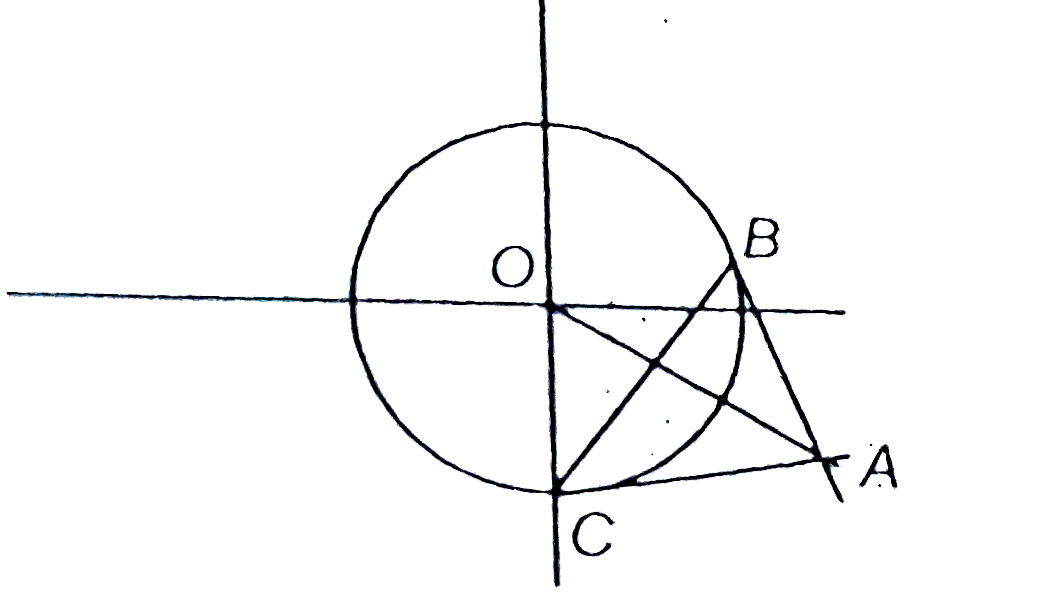
The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 x - 5 y = 20$ to the circle $x^{2} + y^{2} = 9$ is

$20 (x^{2} + y^{2}) - 36 x + 45 y = 0$

$20 (x^{2} + y^{2}) + 36 x - 45 y = 0$

$36 (x^{2} + y^{2}) - 20 y + 45 y = 0$

$36 (x^{2} + y^{2}) + 20 x - 45 y = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video & text solution for The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x^(2) + y^(2) = 9 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Knowledge Check

The chords of contact of the pair of tangents drawn from each point on the line $2 x + y = 4$ to the circle $x^{2} + y^{2} = 1$ pass through the point
A $(1, 2)$
B $(\frac{1}{2}, \frac{1}{4})$
C(2, 4)
Dnone
The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle $x^{2} + y^{2} = 1$ pass through a fixed point
A(2,4)
B(-1/2,-1/4)
C(1/2,1/4)
D(-2,-4)
If the chord of contact of tangents from a point P(h, k) to the circle $x^{2} + y^{2} = a^{2}$ touches the circle $x^{2} + {(y - a)}^{2} = a^{2}$ , then locus of P is
A $y^{2} = a^{2} - 2 a x$
B $y^{2} = a^{2} + 2 a x$
C $x^{2} = a^{2} + 2 a y$
D $x^{2} = a^{2} - 2 a y$

The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 x - 5 y = 20$ to the circle $x^{2} + y^{2} = 9$ is

The correct Answer is:A

Similar Questions

Knowledge Check

The chords of contact of the pair of tangents drawn from each point on the line $2 x + y = 4$ to the circle $x^{2} + y^{2} = 1$ pass through the point

The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle $x^{2} + y^{2} = 1$ pass through a fixed point

If the chord of contact of tangents from a point P(h, k) to the circle $x^{2} + y^{2} = a^{2}$ touches the circle $x^{2} + {(y - a)}^{2} = a^{2}$ , then locus of P is

Recommended Questions

The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line 4x–5y=20 to the circle x2+y2=9 is

The correct Answer is:A

Similar Questions

Knowledge Check

The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle x2+y2=1 pass through the point

The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle x2+y2=1 pass through a fixed point

If the chord of contact of tangents from a point P(h, k) to the circle x2+y2=a2 touches the circle x2+(y−a)2=a2, then locus of P is

Recommended Questions

The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 x - 5 y = 20$ to the circle $x^{2} + y^{2} = 9$ is

The chords of contact of the pair of tangents drawn from each point on the line $2 x + y = 4$ to the circle $x^{2} + y^{2} = 1$ pass through the point

The chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle $x^{2} + y^{2} = 1$ pass through a fixed point

If the chord of contact of tangents from a point P(h, k) to the circle $x^{2} + y^{2} = a^{2}$ touches the circle $x^{2} + {(y - a)}^{2} = a^{2}$ , then locus of P is