The number of nonzero integral values of $a$ for which the function $f (x) = x^{4} + a x^{3} + \frac{3 x^{2}}{2} + 1$ is concave upward along the entire real line is___________

$a \in [0, \infty)$

$a \in (- 2, 2)$

$a \in [- 2, 2]$

$a \in (0, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video & text solution for The number of nonzero integral values of a for which the function f(x)=x^4+a x^3+(3x^2)/2+1 is concave upward along the entire real line is___________ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Knowledge Check

Concavity and convexity :
if $f'' (x) > 0 \forall x \in (a, b)$ then the curve y=f(x) is concave up ( or convex down) in (a,b) and $if f'' (x) < 0 \forall x \in (a, b)$ then the curve y=f(x) is concave down (or convex up ) in (a,b)

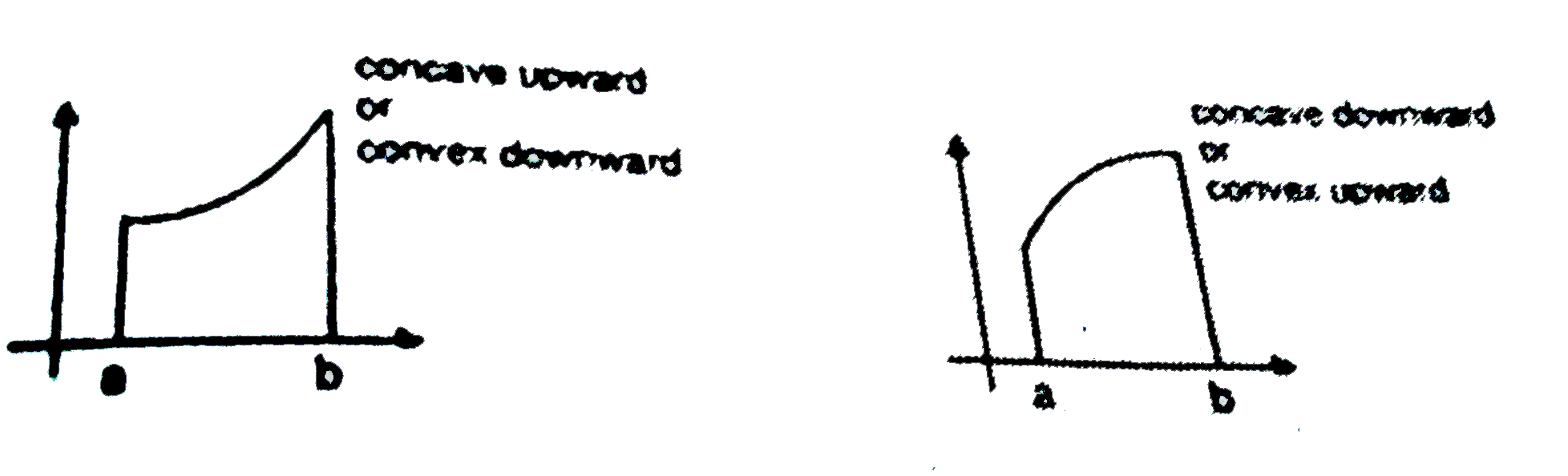
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point $f'' (x)$ is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function $f (x) = x^{4} + a x^{3} + \frac{3 x^{2}}{2} + 1$ will be concave upward along the entire real line is :
A $[- 1, 1]$
B $[- 2, 2]$
C $[0, 2]$
D $[0, 4]$
The number of integral values in the range of the function $f (x) = {sin}^{- 1} x - {cot}^{- 1} x + x^{2} + 2 x + 6$ is
A10
B11
C12
D8
The interval into which the function $y = \frac{x - 1}{x^{2} - 3 x + 3}$ transforms the entire real line is
A $[1 / 3, 2]$
B $[- 1 / 3, 1]$
C $[- 1 / 3, 2]$
Dnone of these

MOTION-MONOTONOCITY-Exercise - 2 (Level-I) ( Objective Problems ) (CURVE SKETCHING, QUESTION ON FINDING NUMBER OF SOLUTIONS )

Home
Ask Doubt
Profile

The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

The number of integral values in the range of the function f(x)=sin−1x−cot−1x+x2+2x+6 is

The interval into which the function y=x−1x2−3x+3 transforms the entire real line is

MOTION-MONOTONOCITY-Exercise - 2 (Level-I) ( Objective Problems ) (CURVE SKETCHING, QUESTION ON FINDING NUMBER OF SOLUTIONS )

The number of nonzero integral values of $a$ for which the function $f (x) = x^{4} + a x^{3} + \frac{3 x^{2}}{2} + 1$ is concave upward along the entire real line is___________

The number of integral values in the range of the function $f (x) = {sin}^{- 1} x - {cot}^{- 1} x + x^{2} + 2 x + 6$ is

The interval into which the function $y = \frac{x - 1}{x^{2} - 3 x + 3}$ transforms the entire real line is