The set Q consists of 15 numbers whose arithmetic mean is zero? Which of the following must also be zero?
I. The median of the numbers in Q.
II. The mode of the number in Q.
III. The sum of the numbers in Q.
I only
II only
III only
I and III only
The correct Answer is:C
To solve the problem, we need to analyze the given information about the set Q consisting of 15 numbers with an arithmetic mean of zero. We will go through each option to determine which must also be zero.
1. Understanding the Arithmetic Mean:
The arithmetic mean (AM) of a set of numbers is calculated as:
AM=Sum of all numbersTotal count of numbers
In this case, the total count of numbers is 15, and we are given that the arithmetic mean is zero.
2. Setting Up the Equation:
Since the arithmetic mean is zero, we can set up the equation:
0=Sum of all 15 numbers15
This implies:
Sum of all 15 numbers=0×15=0
3. Analyzing the Options:
- Option I: The Median of the Numbers in Q:
The median is the middle value when the numbers are arranged in order. The median does not necessarily have to be zero, as it depends on the specific values of the numbers. Therefore, we cannot conclude that the median must be zero.
- Option II: The Mode of the Numbers in Q:
The mode is the number that appears most frequently in the set. Similar to the median, the mode can be any number and does not have to be zero. Thus, we cannot conclude that the mode must be zero.
- Option III: The Sum of the Numbers in Q:
From our earlier calculation, we established that the sum of all 15 numbers is indeed zero. Therefore, this option must be true.
4. Conclusion:
Based on our analysis:
- The sum of the numbers in Q must be zero.
- The median and mode do not necessarily have to be zero.
Thus, the correct answer is:
- Only Option III is correct.
Summary of the Results:
- I. Median: Not necessarily zero.
- II. Mode: Not necessarily zero.
- III. Sum: Must be zero.
The arithmetic mean (AM) of a set of numbers is calculated as:
AM=Sum of all numbersTotal count of numbers
In this case, the total count of numbers is 15, and we are given that the arithmetic mean is zero.
Since the arithmetic mean is zero, we can set up the equation:
0=Sum of all 15 numbers15
This implies:
Sum of all 15 numbers=0×15=0
- Option I: The Median of the Numbers in Q:
The median is the middle value when the numbers are arranged in order. The median does not necessarily have to be zero, as it depends on the specific values of the numbers. Therefore, we cannot conclude that the median must be zero.
The mode is the number that appears most frequently in the set. Similar to the median, the mode can be any number and does not have to be zero. Thus, we cannot conclude that the mode must be zero.
From our earlier calculation, we established that the sum of all 15 numbers is indeed zero. Therefore, this option must be true.
Based on our analysis:
- The sum of the numbers in Q must be zero.
- The median and mode do not necessarily have to be zero.
- Only Option III is correct.
- I. Median: Not necessarily zero.
- II. Mode: Not necessarily zero.
- III. Sum: Must be zero.
Similar Questions
Knowledge Check
Which of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
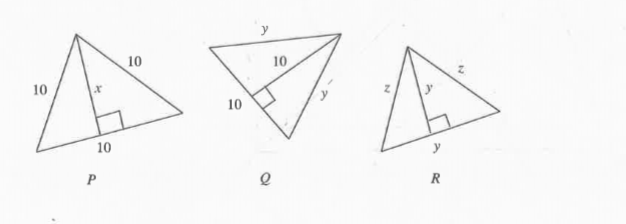 AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt IIThe mean of a finite set S of numbers is 14, the median of this set of numbers is 12, and the standard deviation is 1.8. A new set T is formed by multiplying each member of the set S by 3. Which of the following statements must be true of the set T ?
I. The mean of the numbers in set T is 42.
II. The median of the numbers in set T is 36.
III. The standard deviation of the numbers in set T is 5.4.AI onlyBII onlyCI and II onlyDI, II, and IIIIf p is the sum of q and r, then which one of the following must equal q -r ?
Ap−rBp+rCp−2rDp+2r
Q∪Z=Q, where Q is the set of rational numbers and Z is the set of integers.
View SolutionSymbolise the following statements.
The square roots of all prime numbers are irrational numbers. ( Let P denote the set of prime numbers and Q that of irrational numbers ).
View SolutionFor every pair of natural number n and m, to which of the following sets must n + m belong?
I. The natural numbers
II. The intergers
III. The rational numbers
IV. The real numbers
V. The complex numbers
View SolutionWhich of the following sets of real numbers is such that if x is an element of the set and y is an element of the set, then the sum of x and y is an element of the set ?
I. The set of negative integers
II. The set of rational numbers
III. The set of irrational numbers
View SolutionThe following diagram represents the solution of two sets P and Q on the number line:
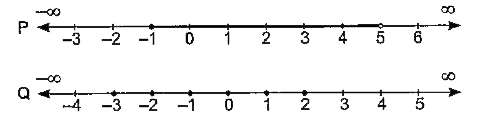
The solution set of Q in set builder form is:
View Solution
