The probability distribution of a random variable X is given below, then k=
X=x1234P(X=x)k4k4kkSolution in Telugu
0.1
0.2
0.3
0.4
The correct Answer is:A
Step by step video, text & image solution for The probability distribution of a random variable X is given below, then k= {:(X=x,1,2,3,4),(P(X=x),k,4k,4k,k):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEORETICAL DISTRIBUTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 1 (CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVE 1,2,3 OR 4 GIVEN )
153 Videos
- THEORETICAL DISTRIBUTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -1)
4 Videos
- THE PLANEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THE PLANEEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET 4
4 Videos
- THEORY OF EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 4
4 Videos
Similar Questions
A random varible X has its range :1,2,3}. If P(X=1)=c,P(X=2)=3c,P(X=3)=5c, then c=
View SolutionA random variable X follows the following distribution
(X=xi:,0,1,2,3),(P(X=xi):,2/6,3/6,0/6,1/6,)
The mean and the variance are
View SolutionA: The equation of the plane passing through the point (- 1, 2, 4) and parallel to the plane 2x + 3y – 5z +6=0 is 2x + 3y - 5z + 16 = 0.
R: The equation of the plane passing through the point (x1,y1,z1) and parallel to the plane ax + by + cz +d=0 is a(x–x1)+b(y−y1)+c(z−z1)=0
View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.
View SolutionThe probability distribution of a discrete random variable X is given below
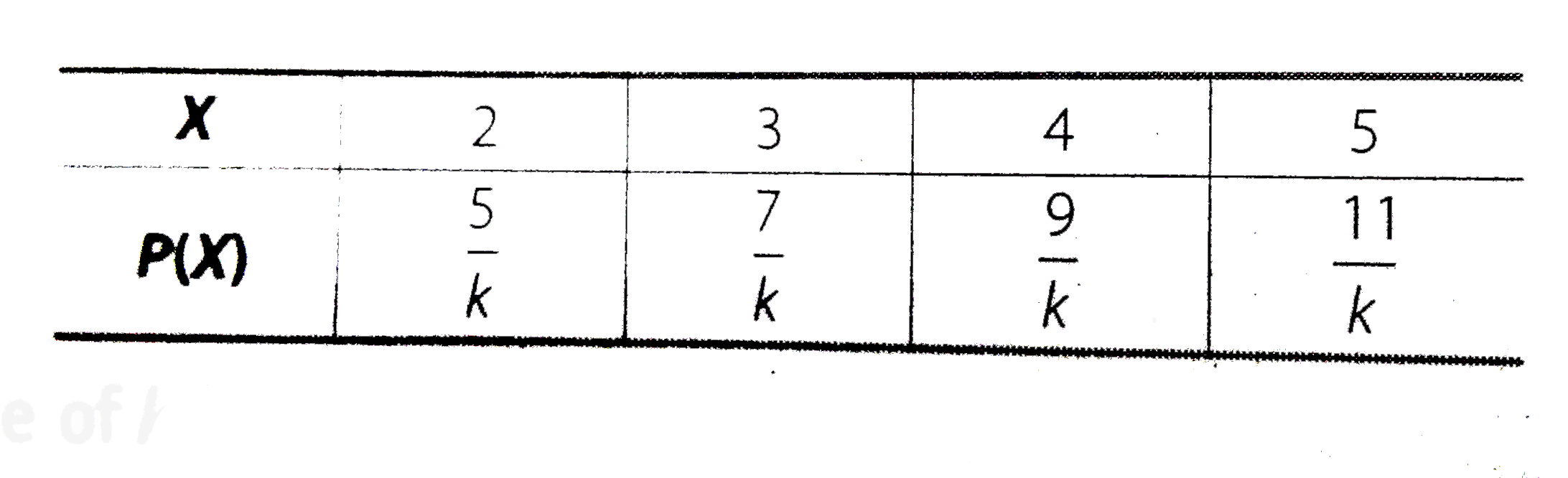
The value of k is
View SolutionThe probability distribution of a random variable X is given below , then k=
X=x1234P(X=x)2k4k3kk
View SolutionA random variable X has the following distribution
X=x1:1234P(X=x1):k2k3k4k
The value of k and P(X<3) are equal to
View SolutionA random variable X has the probability distribution given below. Its variance is
X12345P(X=x)k2k3k2kk
View SolutionThe prabability distribution of a random variable x is given below
x=k01234p(x=k)0.10.40.30.20
The variance of X is
View SolutionA random variable x has the following distribution .
x1234f(x)k2k4k3k
Then its mean is :
View SolutionThe probability distribution of a discrete random variable X is given below
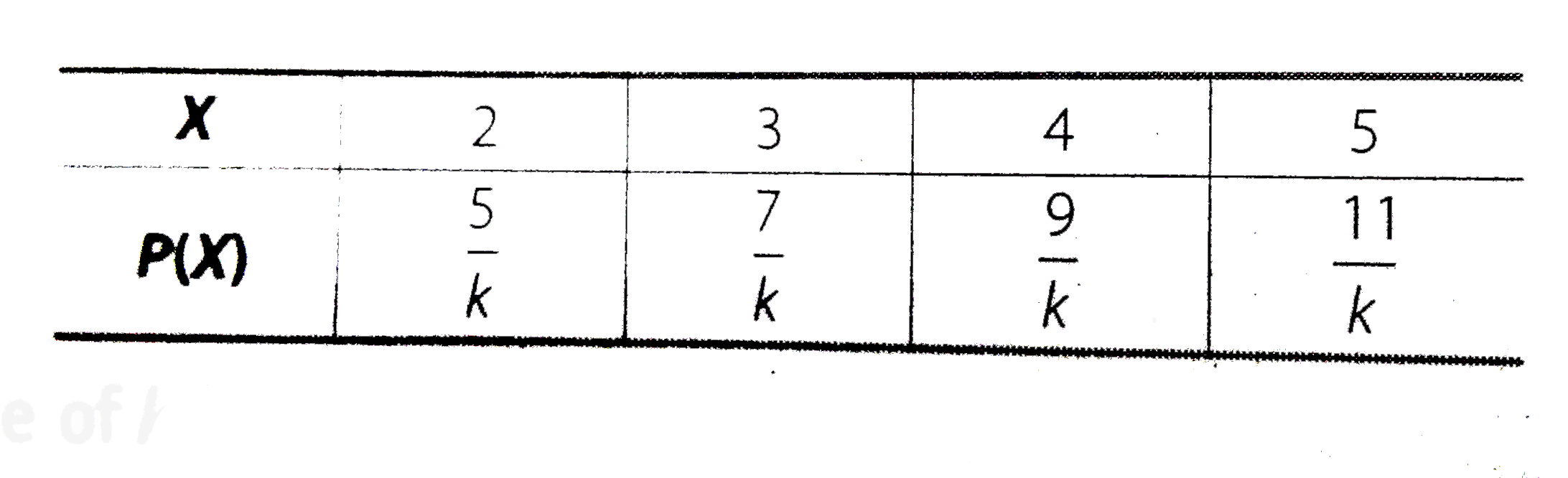
The value of k is
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
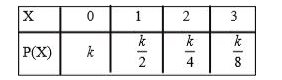
k का मान निर्धारित कीजिए,
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता- बंटन नीचे दिया हुआ है:
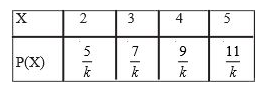
k का मान है,
View SolutionThe probability distribution of a discrete random variable X is given below :
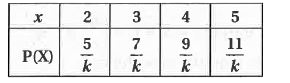
The value of k is .........
View Solution
