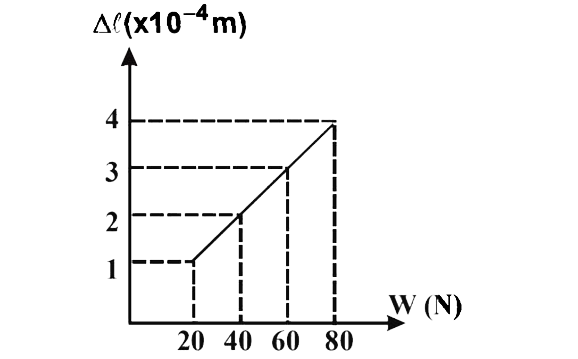
The graph shows the extension of a wire of length 1m suspended from th

The adjacent graph shows the estension $(Δ l)$ of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is $10^{- 6} m^{2}$ , calculate the Young's modulus of the material of the wire.

A(a) $2 \times 10^{11} N / m$
B(b) $2 \times 10^{- 11} N / m$
C(c) $3 \times 10^{- 12} N / m$
D(d) $2 \times 10^{- 13} N / m$
The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .

A $2 \times 10^{11} N m^{- 2}$
B $2 \times 10^{- 11} N m^{- 2}$
C $3 \times 10^{- 12} N m^{2}$
D $2 \times 10^{- 13} N m^{2}$
A steel wire 4.0 m in length is stretched through 2.0 mm. The cross-sectional area of the wire is $2.0 m m^{2}$ . If young's modulus of steel is $2.0 \times 10^{11} N m^{- 2}$ , then find the energy density of wire.
A $2.5 \times 10^{4} J m^{- 3}$
B $0.5 \times 10^{4} J m^{- 3}$
C $1.6 \times 10^{4} J m^{- 3}$
D $3.6 \times 10^{4} J m^{- 3}$

$Y = \frac{F / A}{Δ l / l} = \frac{W l}{A Δ l} \Rightarrow \frac{W}{Δ l} = \frac{Y A}{l} =$ slope
$\Rightarrow Y = \frac{l}{A}$ (slope) $= \frac{1}{10} (\frac{40 - 20}{(2 - 1) \times 10^{- 3}})$
$= 2 \times 10^{10} N m^{- 2}$