Three masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be

Video Solution

Text Solution

Verified by Experts

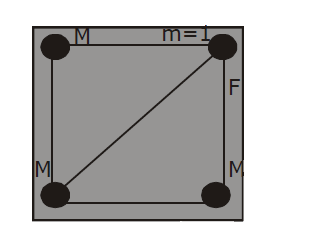
Force on m = 1 due to masses at corner 1 and 3 are $- \to F_{1}$ and $- \to F_{3}$ with $F_{1} = F_{3} = \frac{GM}{a^{2}}$ resultant of $- \to F_{1}$ and $- \to F_{3}$ is $F_{r} = \sqrt{2} \frac{GM}{a^{2}}$ and its direction is along the diagonal
Force on m due to mass M at 2 is
$F_{2} = \frac{GM}{{(\sqrt{2 a})}^{2}} = \frac{GM}{2 a^{2}}$ , $F_{r}$ and $F_{2}$ act in the same direction. Resultant of these two is the net force:
$F_{net} = \frac{\sqrt{2} GM}{a^{2}} + \frac{GM}{2 a^{2}} = \frac{GM}{a^{2}} [\sqrt{2} + \frac{1}{2}]$ , it is directed along the diagonal as shown in the figure.

Updated on:21/07/2023

Equal charges q are placed at the three corners B, C, D of a square ABCD of side a. The potential at A is
A $\frac{1}{4 π ε_{0}} \frac{q}{a}$
B $\frac{3 q}{4 π ε_{0}}$
C $\frac{q}{4 π ε_{0} a} [2 + \frac{1}{\sqrt{2}}]$
D $\frac{q}{4 π ε_{0} a} [1 + \sqrt{2}]$
Equal charges q are placed at the three corners B, C, D of a square ABCD of side 'a'. The ratio of potential at A to centre O is
A $\frac{2 \sqrt{2} + 1}{3 \sqrt{2}}$
B $\frac{2 + \sqrt{2}}{6}$
C $\frac{2 \sqrt{2} + 1}{6}$
D $\frac{2 \sqrt{2} + 1}{3}$
Three equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
A $\frac{G m^{2}}{a^{2}}$
B $\frac{4 G m^{2}}{3 a^{2}}$
C $\frac{3 G m^{2}}{a^{2}}$
Dzero