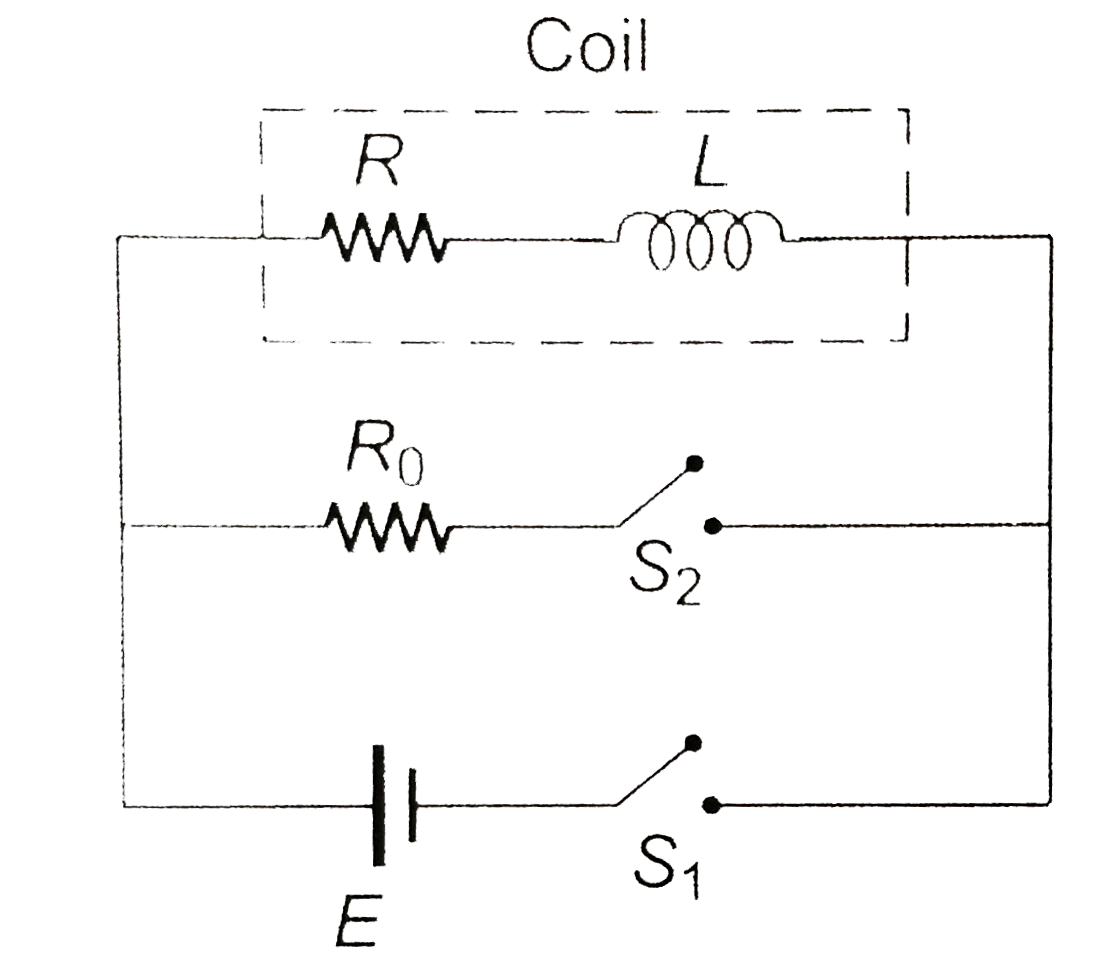
At t=0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
(i) The current through the capacitor immediately after that moment
(ii) Charge on the capacitor long after that moment.
(iii) Total charge flown through the cell of emf 2ε after S2 is closed.
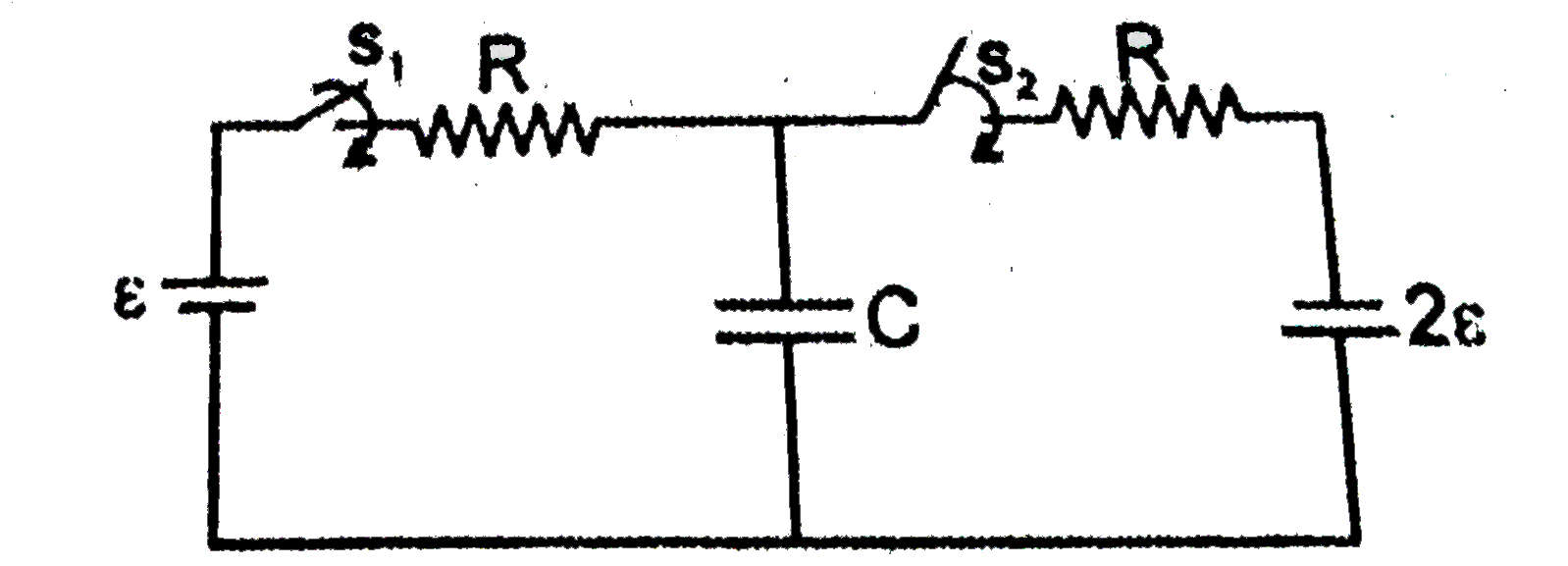
(i) Let Potential at point A is zero . The potential at point B and C will be ∈ (because current through the circuit is zero )
VB−VA=(∈−0)
∴ Charge on capacitor = C = (∈−0)=C∈
(##MOTCONJ∃PHYC25SLV037_S01.png width=80%>Now S_ 2 isclosedand S_1isopen<br>(p.d.across∩aci→randchar≥onitwill¬chan≥suddenly)<br>PotentialatAisZerosoatDitis−2in <br> therefore " " Currentthroughthe∩aci→r<br> " " = ( in -( 2in ))/( R) =( 3in )/(R) (B"to " D) <br>(ii)afteralongtime,i=0<br> V_a -V_A =V_D -V_A =-2in <br> therefore " "Q =C( -2in -0) =- 2in C <br> (##MOT_CON_JEE_PHY_C25_SLV_037_S02.png" width="80%">
(iii) The charge on the lower plate (which is connected to the battery ) changes from −∈Cto 2∈C
∴ this charge will come from the battery
∴ charge flown from that cell is 2∈C downward
(##MOT_CON_JEE_PHY_C25_SLV_037_S03.png" width="80%">
Topper's Solved these Questions
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -1
60 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -2
36 Videos
- CALORIMETRY BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B
4 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
Similar Questions
At t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
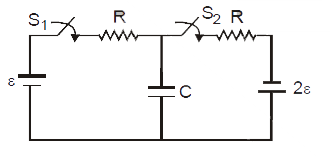
The current through the capacitor immediately after that moment
View SolutionAt t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out

Charge on the capacitor long after that moment.
View Solution
Knowledge Check
In the circuit diagram the current through the battery immediately after the switch S is closed is
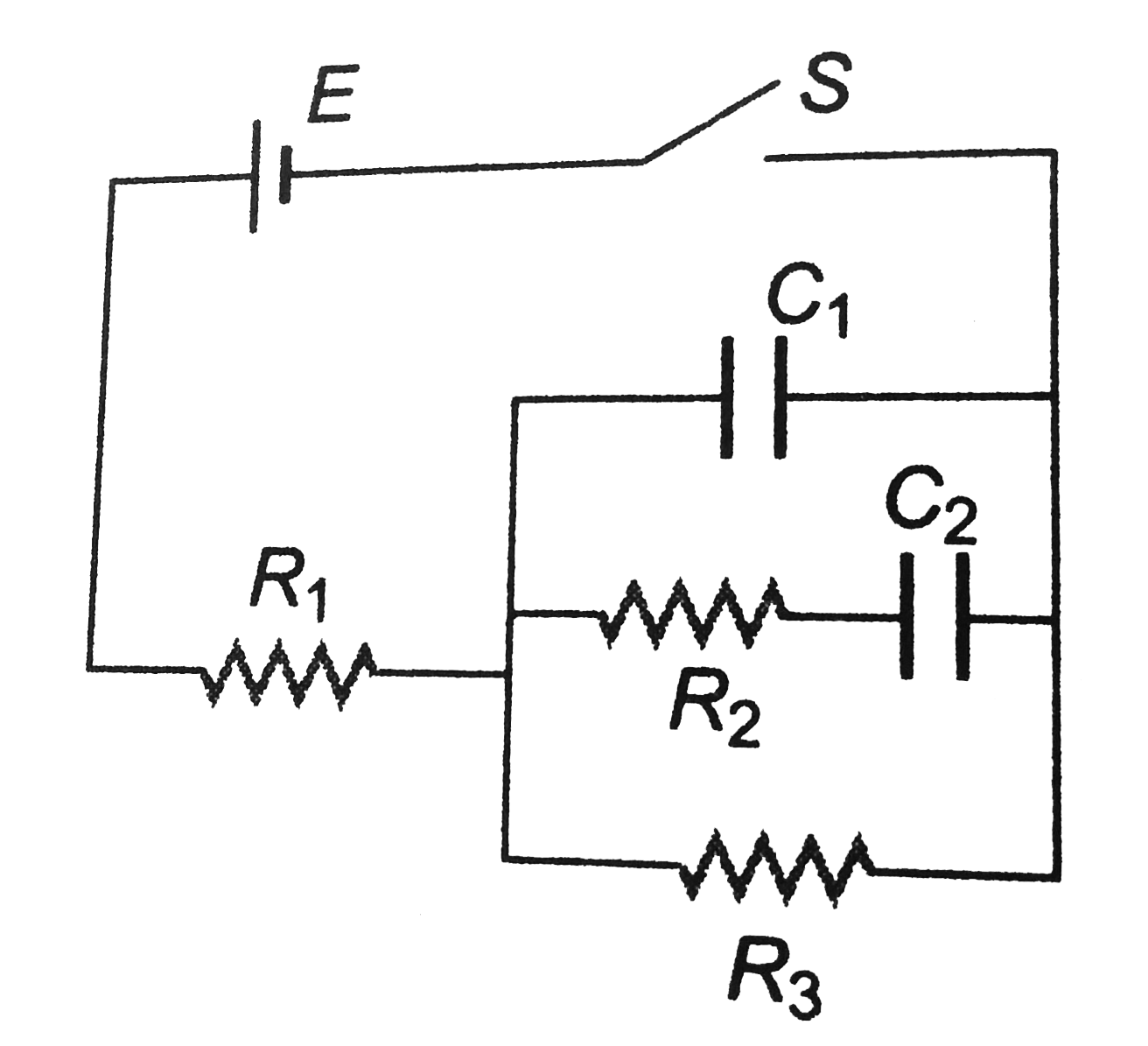 AzeroBER1CER1+R2DER1+R2R3R2+R3
AzeroBER1CER1+R2DER1+R2R3R2+R3As shown in diagram initial charge on capacitor is zreo . Now switch S1 is closed & it remains closed for a long time but S2 remains open . Now switch S1 is opened & switch S2 is closed at t=0, then after closing the switch S2 :
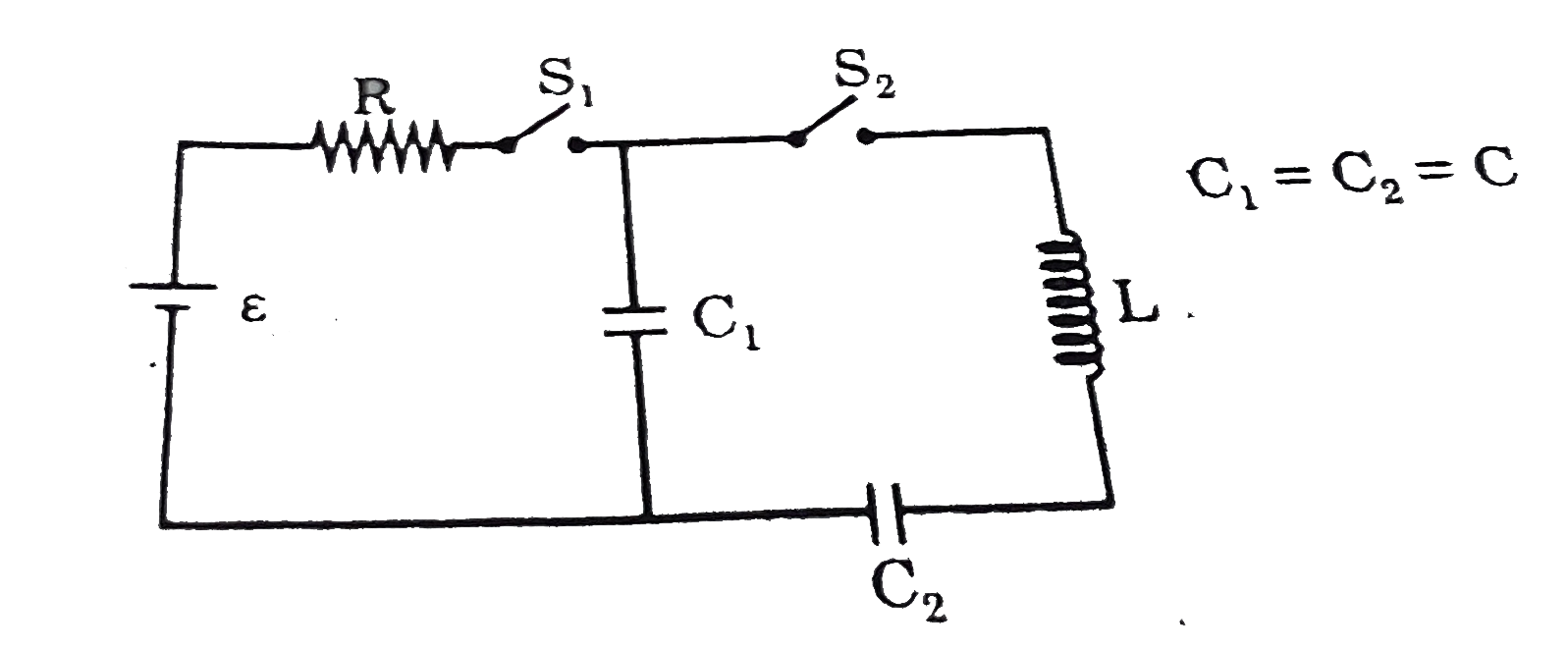 AMaximum current passing through inductor will be (ε)√C2L.BMaximum magnitude of rate of change of current through inductor will be εL.CMaximum charge on capacitor C2 will be εC.DMaximum charge on capacitor C2 will be εC2.
AMaximum current passing through inductor will be (ε)√C2L.BMaximum magnitude of rate of change of current through inductor will be εL.CMaximum charge on capacitor C2 will be εC.DMaximum charge on capacitor C2 will be εC2.In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
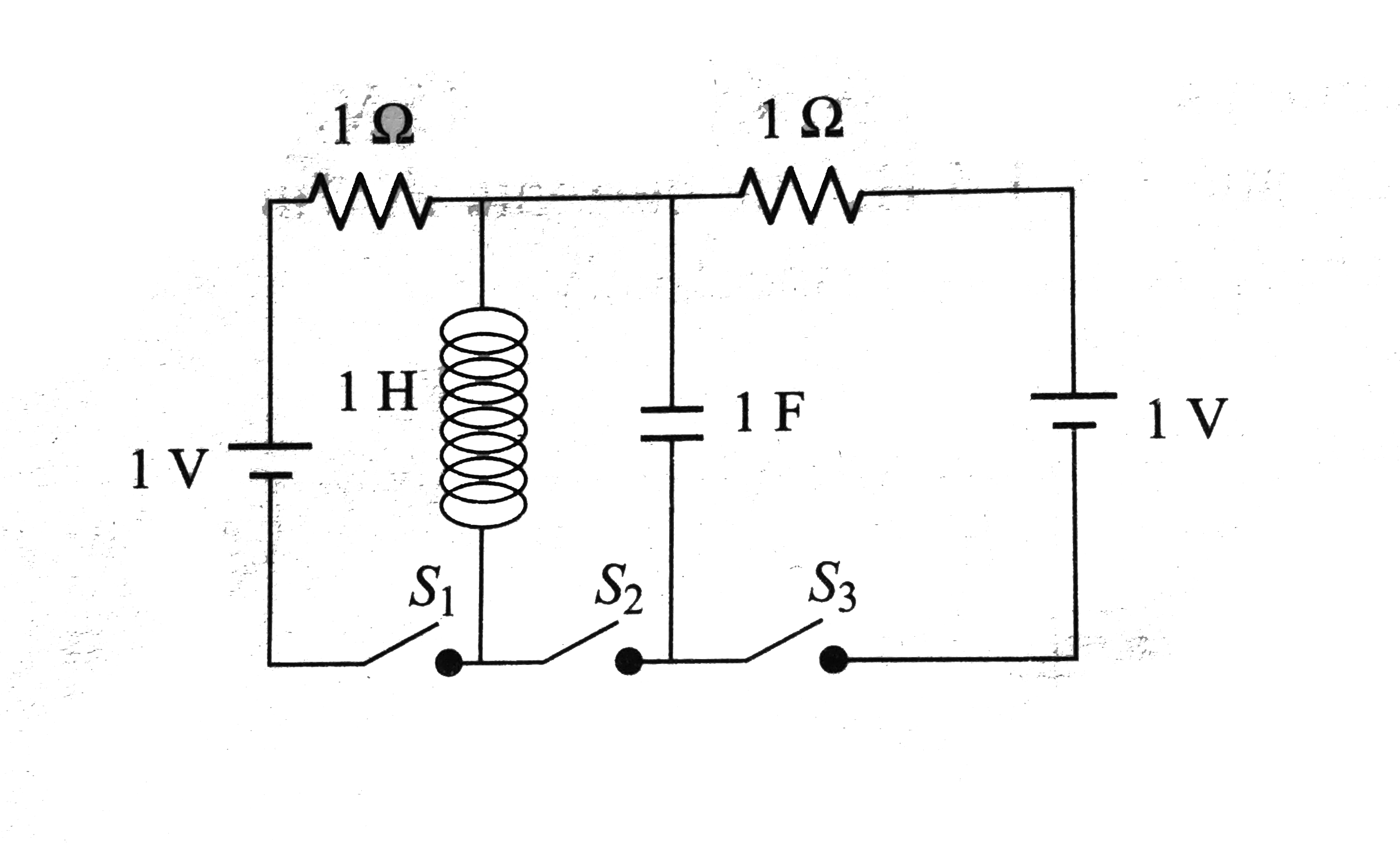
the maximum charge on the capacitorA√3(1+1e)B√3(1−1e)C√2(1+1e)D√2(1−1e)
At t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
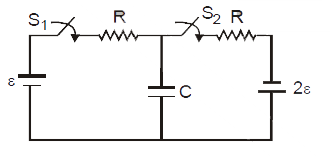
Total charge flown through the cell of emf 2ε after S2 is closed.
View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View Solution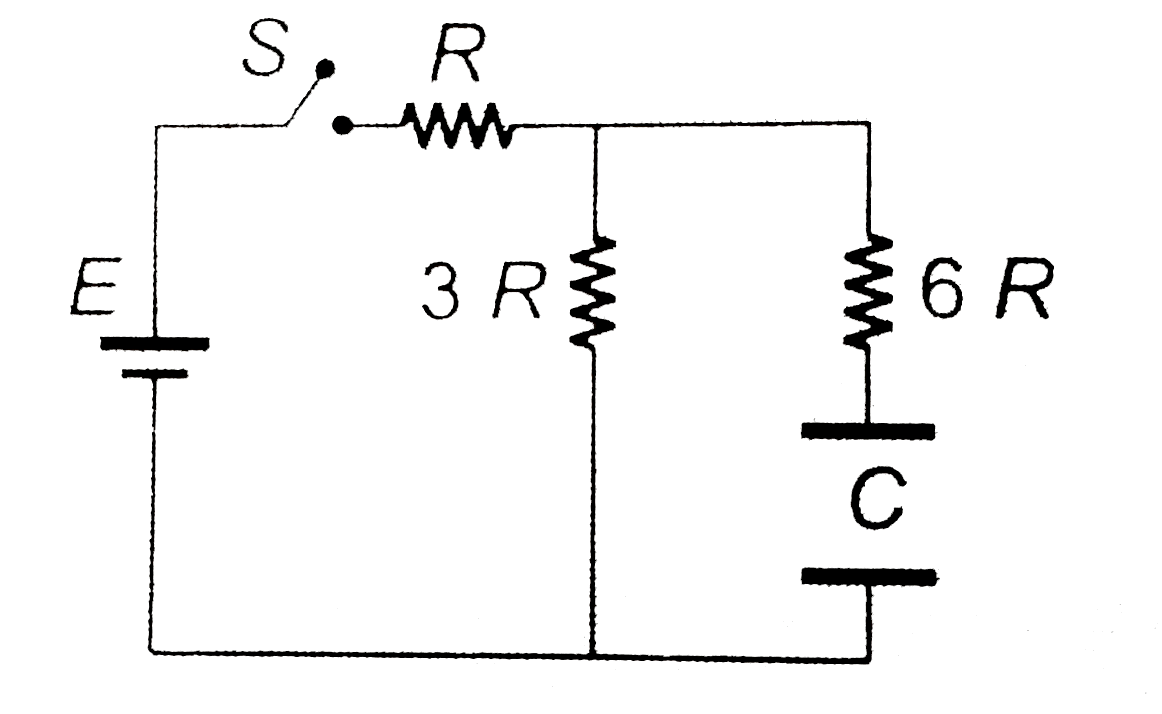
Find currents through resistors
(i) immediately after closing the switch
(ii) after a long time.
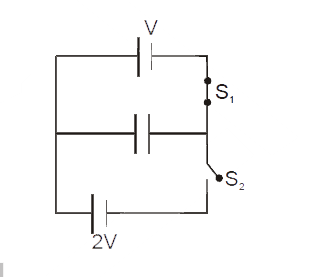
View SolutionAt any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
View Solution
