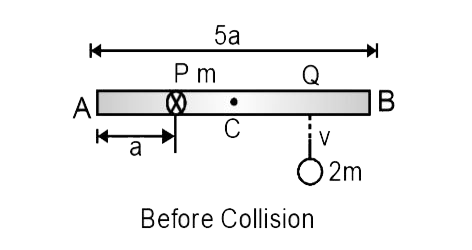
A uniform rod AB of mass m and length 5a is free to rotate on a smooth horizontal table about a pivot through P, a point on AB such that AP = a. A particle of mass 2m moving on the table strikes AB perpendicularly at the point 2a from P with speed v, the rod being at rest. If the
coefficient of restitution between them is14 , find
their speeds immediately after impact.
Let the point of impact be Q so that
PQ = 2a
Let P be the point of pivot that AP = a
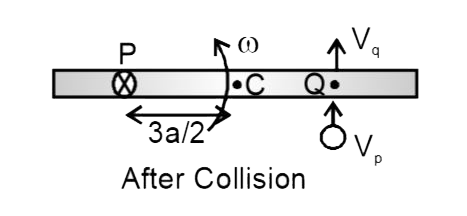
Let the velocities of point, Q and the particle after impact
be vqandvp respectively then from momentum conservation about point P.
L1=Lf
2a(2mv)=Ipω+(2a)(2mvp) ...(i)
lp=13m(5a2)2+m(3a2)2 {use parallelaxis theorem}
=13ma23 ...(ii)
use equation (ii) in equation (i)
4ma(v−vp)=13ma23ω
12(v−vp)=13aω (iii)
coefficient of restitutione e=velocity of seperationvelocity of approach
14=vq−vpv
⇒vq−vp=v4 ...(iv)
vq=2aω ...(v)
Put value of ω from eq (iii) to equation(v)
vq=2(1213)(v−vp)
So now from equation (iv)
2413(v−vp)−vp=v4⇒vp=83v148
So in this way get ω=15v37a
Topper's Solved these Questions
Similar Questions
A uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution
Knowledge Check
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+mA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
A2MvM−mB2mvM+mCMvM+mDmvM+mA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+m
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass C before the collision.
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

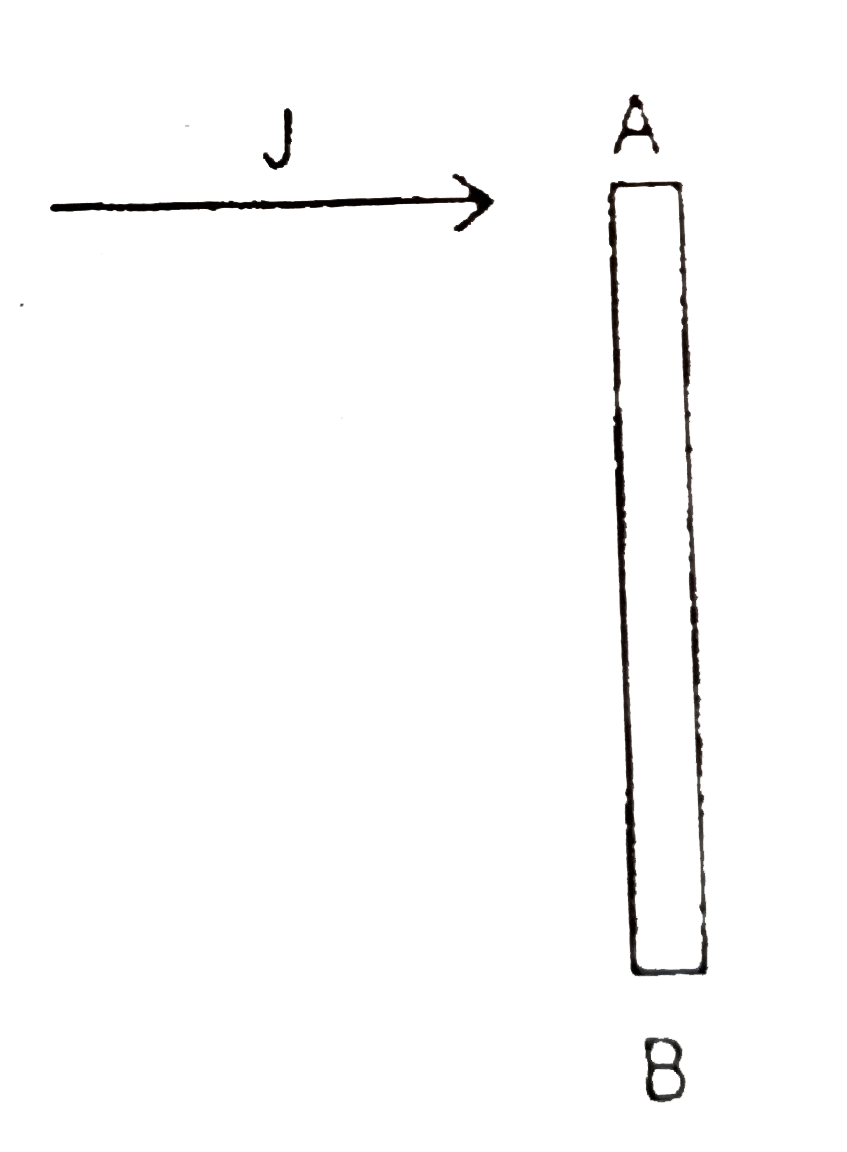
View SolutionA rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
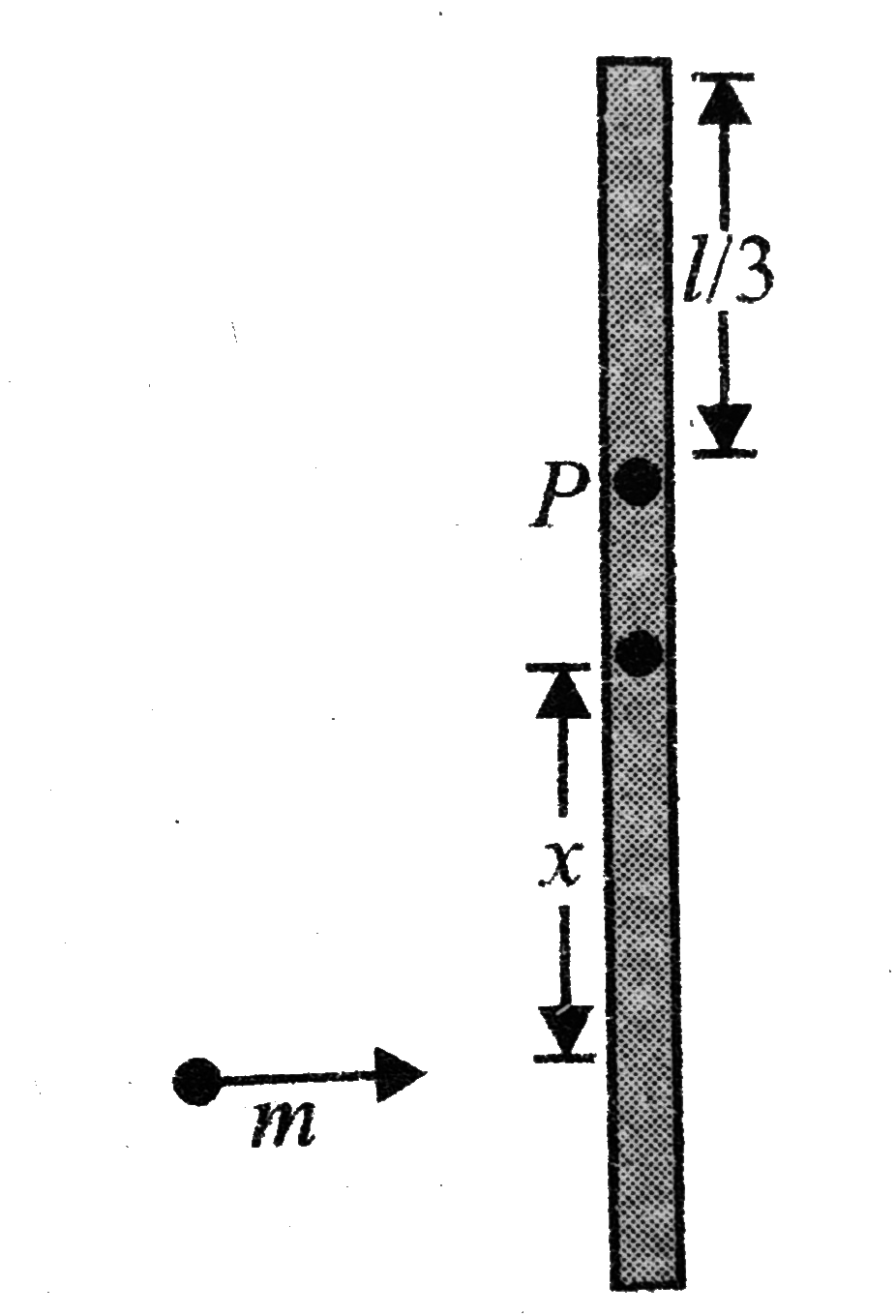
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View Solution
