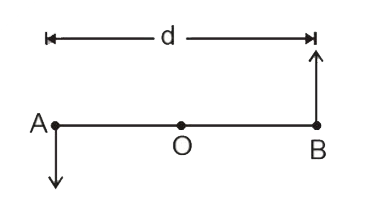
Two small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed . Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
Consider the situation shown in figure. The velocity of the ball A with respet to the centre O is .
The angular momentum of the ball with respect to the axis is
. The same the angular momentum of the second ball. The angular momentum of the system is equal to sum of these two angular momenta i.e., .
Topper's Solved these Questions
Similar Questions
Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View Solution
Knowledge Check
Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
A23mωL2B13ω2LmC23ω2LmD13LmTwo particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
AqmB2qmCq2mDqπmTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
Aq2mBqmC2qmDqπm
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.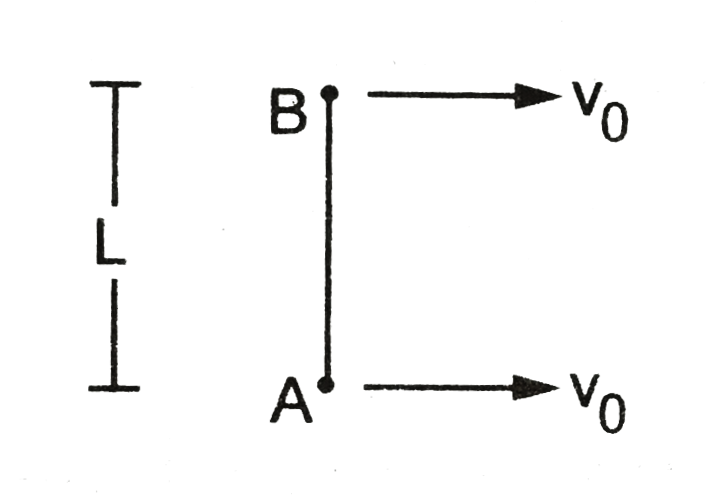
View SolutionA uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
the angular speed of the rod about the centre of mass,
View SolutionTwo small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo point masses A of mass M and B of mass of 4M are fixed at the ends of a rod of length l and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass A is at
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View Solution
