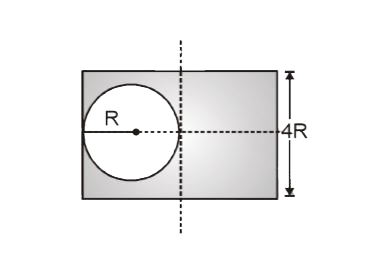
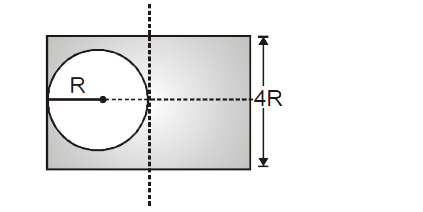
Find the position of centre of mass of the uniform lamina shown in figure.
Video Solution
Text Solution
Hence,
area of complete circle
area of small circle
coordinates of centre of mass of large circle and coordinates of centre of mass of small circle
Using
we get
and as both are zero.
Therefore, coordinates of COM of the lamina shown in figure are
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 171videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)40videos
CENTRE OF MASS
- BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II19videos
Capacitance
- BOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 416videos
CIRCULAR MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
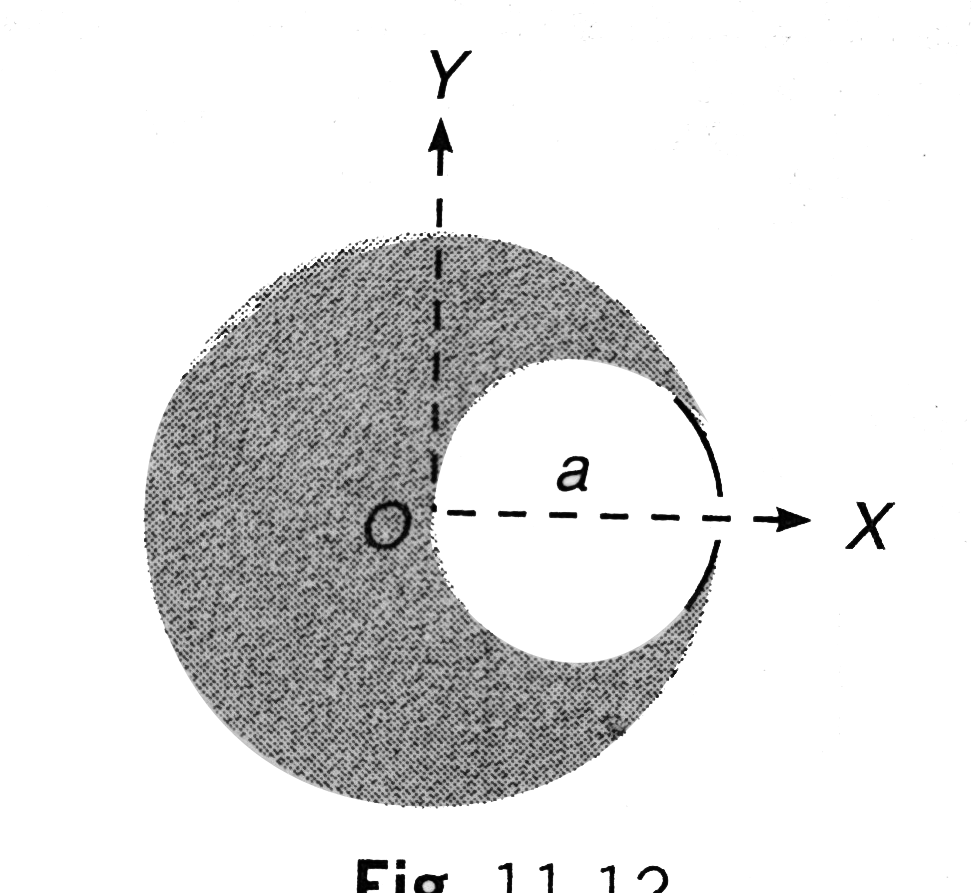
Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius a2 is cut from disc of radius a.
 A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0)
A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0) - Question 2 - Select One
Which of the following points is the likely position of the centre of mass of the system shown in figure?
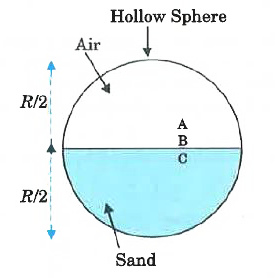 AA pencilBBCCDD
AA pencilBBCCDD - Question 3 - Select One
Find the x coordinate of the centre of mass of the bricks shown in figure :
 A2425lB2524lC1516lD1615
A2425lB2524lC1516lD1615
Find the position of centre of mass of the uniform planner sheet shown in figure with respect to the origin (O) -
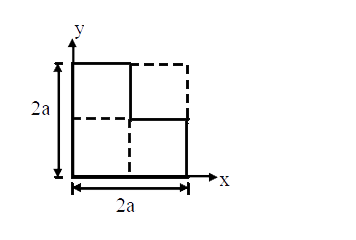 View Solution
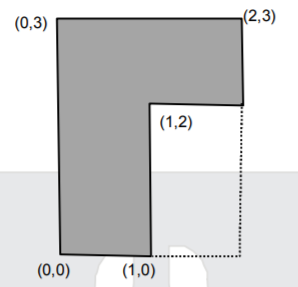
View SolutionFind the position of centre of mass of the section shown in figure
 View Solution
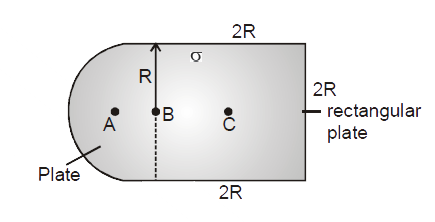
View SolutionFind the co-ordinates of centre of mass of the lamina shown in figure
 View Solution
View SolutionFind out the position of centre of mass of the figure shown below.
View SolutionLocate the position of centre of mass of a uniform plate of Mass m as shown in fig 4E 34
 View Solution
View Solution