Compute the area of the figure bounded by the straight lines $= 0, x = 2$ and the curves $y = 2^{x}, y = 2 x - x^{2} .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $= \frac{3}{ln 2} - \frac{4}{3}$ sq. units.

Updated on:21/07/2023

Answer

Step by step video & text solution for Compute the area of the figure bounded by the straight lines =0,x=2 and the curvesy=2^x ,y=2x-x^2dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

AREA UNDER THE CURVEBOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 1
17 Videos
AREA UNDER THE CURVEBOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 2 (LEVEL-I)
25 Videos
BASIC MATHEMATIC & LOGARITHM BOOK - MOTIONCHAPTER - BASIC MATHEMATIC & LOGARITHM EXERCISE - Exercise - 4
4 Videos

Knowledge Check

The area of the figure bounded by the curves $y^{2} = 2 x + 1$ and $x - y - 1 = 0$ , is
A $2 / 3$
B $4 / 3$
C $8 / 3$
D $16 / 3$

The area of the region bounded by the straight lines $y = x, y = 2 x$ and $y = 2$ ,is
View Solution
$The area of the region bounded by the straight lines y = x, y = 2 x and y = 2,is$
View Solution
Compute the area of the figure bounded by the parabolas $x = - 2 y^{2}, x = 1 - 3 y^{2}$

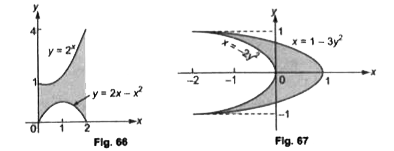
View Solution
Compute the area of the figure bounded by the curve $\sqrt{x} + \sqrt{y} = 1$ and the straight line $x + y = 1$
View Solution
Find the area of the figure bounded by the curve $y = {sin}^{- 1} x$ , the lines $x = 0$ and $y = \frac{π}{2}$ .
View Solution
The area of the region bounded by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
View Solution
Find the area of the region bounded by the curves $y = x^{2} + 2$ , $y = x, x = 0$ and $x = 3$ .
View Solution

MOTION-AREA UNDER THE CURVE-EXERCISE - 4 LEVEL - II

Compute the area of the figure bounded by the straight lines =0,x=2...
03:31
Let g(x) = cosx^(2), f(x) = sqrt(x), and alpha, beta (alpha lt beta)...
05:48
The area of the region between the curves y= sqrt((1+sinx)/(cosx))and ...
07:21
Consider the function defined implicitly by the equation y^3-3y+x=0 on...
05:17
Consider the functions defined implicitly by the equation y^(3) – 3y +...
04:29
Consider the functions defined implicitly by the equation y^(3) – 3y +...
04:29
Area of the region bounded by the curve y=e^(x) and linesx=0 and y=e i...
06:46
Let the straight line x = b divide the area enclosed by y = (1-x)^(2),...
05:54
Let f:[-1,2]vec[0,oo) be a continuous function such that f(x)=f(1-x)fo...
02:17
Let S be the area of the region enclosed by y=e^-x^2,y=0,x=0,a n dx=1....
04:32
The area enclosed by the curves y= sinx+cosx and y = | cosx-sin x | ov...
05:21
Let F(x)=intx^[x^2+pi/6][2cos^2t.dt] for all x in R and f:[0,1/2] -> [...
05:38
Area of region {(x,y) in R^(2): y ge sqrt(|x+3|,)5y le x + 9 le 15}
03:11
If the line x= alpha divides the area of region R={(x,y)in R^(2): x^(...
06:10
A farmer F1 has a land in the shape of a triangle with vertices at ...
03:11

Home
Ask Doubt
Profile

Compute the area of the figure bounded by the straight lines =0,x=2 and the curvesy=2x,y=2x−x2.

The correct Answer is:=3ln2−43 sq. units.

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the figure bounded by the curves y2=2x+1 and x−y−1=0 , is

MOTION-AREA UNDER THE CURVE-EXERCISE - 4 LEVEL - II

Compute the area of the figure bounded by the straight lines $= 0, x = 2$ and the curves $y = 2^{x}, y = 2 x - x^{2} .$

The correct Answer is: $= \frac{3}{ln 2} - \frac{4}{3}$ sq. units.

The area of the figure bounded by the curves $y^{2} = 2 x + 1$ and $x - y - 1 = 0$ , is