If a line L touches the circle x2+y2+8x+15=0 at A in second quadrant and circle x2+y2−12x+32=0 at B in fourth quadrant and d is distance between A and B then d2 is:
The correct Answer is:91
C1D2=C1C22−C2D2=100−9=91
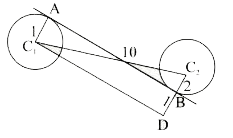 .
.
Similar Questions
Knowledge Check
- Question 1 - Select One
Circle x2+y2−8x+4y+4=0 touches
AX-axisBY-axisCboth X-axis and Y-axisDnone of the axes - Question 2 - Select One
If line 3x−y+c=0 touches circle x2+y2−2x+8y−23=0 , then c =
A13,-27B−13,27C13,27D−13,−27 - Question 3 - Select One
(i) Centre of the circle x2+y2−8x+10y+12=0 is
Centre of the circle 2x2+2y2−x=0 is :A(12,0)B(−12,0)C(14,0)D(−14,0)
The line 4y−3x+λ=0 touches the circle x2+y2−4x−8y−5=0 then λ=
View SolutionFind the area enclosed between circle x2+y2=1 and the line x+y=1 in first quadrant.
View Solution(i) Find the equation of a circle , which is concentric with the circle x2+y2−6x+12y+15=0 and of double its radius.
(ii) Find the equation of a circle , which is concentric with the circle x2+y2−2x−4y+1=0 and whose radius is 5.
(iii) Find the equation of the cricle concentric with x2+y2−4x−6y−3=0 and which touches the y-axis.
(iv) find the equation of a circle passing through the centre of the circle x2+y2+8x+10y−7=0 and concentric with the circle
2x2+2y2−8x−12y−9=0.
(v) Find the equation of the circle concentric with the circle x2+y2+4x−8y−6=0 and having radius double of its radius.View SolutionThe circle x2+y2−8x+4y+4=0 touches
View SolutionIf the circle x2+y2+4x+2y+c=0 bisects the cirucumference of the cirlce x2+y2−2x−8y−d=0 then c + d =
View Solution
