Resultant of two vectors →Aand→B is of magnitude P, If →B is reversed, then resultant is of magnitude Q. What is the value of P2+Q2 ?
2(A2+B2)
2(A2+B2)
A2−B2
A2+B2
The correct Answer is:A
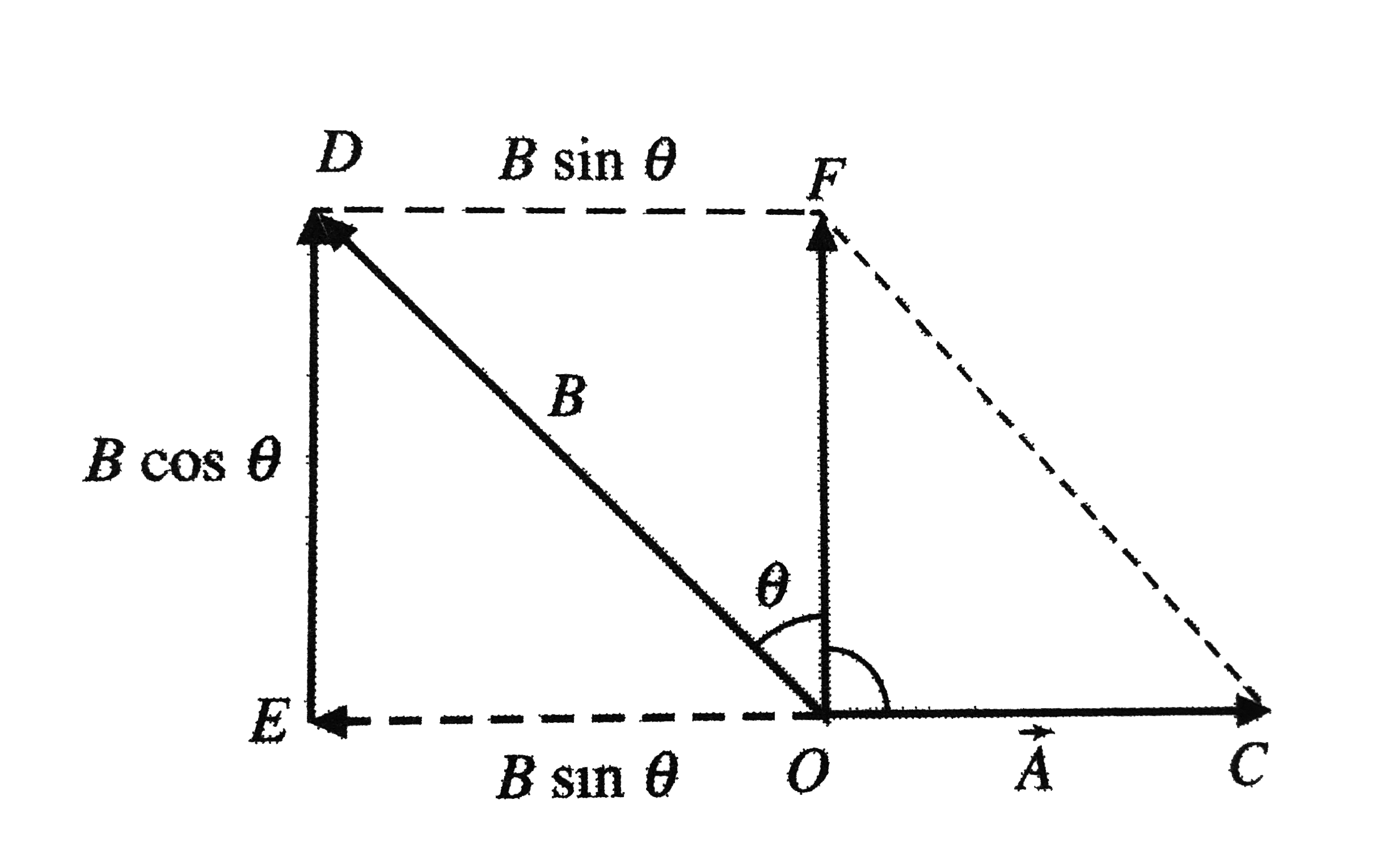
Let θ be angle between →Aand→B
∴ Resultant of →Aand→B is p=√A2+B2+2ABcosθ ……(i)
When is reversed, then the angle between →Aand→B is (180∘−θ).
∴ Resultant of →Aand→B is Q=√A2+B2+2ABcos(180∘−θ)
Q=√A2_B2+2ABcosθ
Squaring and adding (i) and (ii), we get P2+Q2=2(A2+B2).
Similar Questions
The resultant of two forces F1andF2 is P. If F2 is reversed , then resultant is Q . Then the value of (P2+Q2) in terms of F1andF2 is
View SolutionTwo foreces →Pand→Q are acting at a point . If →P is reversed, the new resultant becomes between magnitudes of P and Q is given by P=KQ. Find k.
View Solution
Knowledge Check
If →A+→B=→C, then magnitude of →B is
A→C−→ABC-AC√→C.→B−→A.→BD√→C.→A−→B.→AThe resultant of two vectors →Aand→B is →C. If the megnitude of →B is doubled, the new resultant vector becomes perpendicular to →A, then the magnitude of →C is
A2BBBC3BD4BWhen two vectors →A and →B of magnitudes a and b respectively are added, the magnitude of resultant vector is always
AEqual to (a+b)BLess than (a+b)CGreater than (a+b)DNot greater than (a+b)
The maximum value of the magnitude of the resultant of two vectors →Pand→Q is 24 units and the minimum value of the magnitude of their resultant is 4 units. What is the ratio of the magnitudes of the vectors →Pand→Q ?
View SolutionThe resultant of two vectors →P and →Q is →R. If the magnitude of →Q is doubled, the new resultant vector becomes perpendicular to →P. Then, the magnitude of →R is equal to
View SolutionThe resultant of →A&→B is →R1. On reversing the vector →B, the resultant becomes →R2. What is the value os R21+R22 ?
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .
.
View SolutionResultant of two vectors of magnitude P and Q is of magnitude Q.If the magnitude of →Q is doubled now the angle made by new resultant with →P is
View Solution
