The system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.

(a) π10 sec , (b) 4 cm (c ) 2.40 kg m /sec
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -3 (Leve-I) ( SECTION - D ) ( Combination of springs )
Explore 2 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -3 (Leve-I) ( SECTION - E,F ) ( Angu lar shm & s imple pendulum )
Explore 2 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -3 (Leve-I) ( SECTION - B ) ( Time per iod and angular frequency in SHM )
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
The system shown in the figure can move on a smooth surface. They are initially compressed by 6cm and then released, then choose the correct options.

(a) The system performs, SHM with time period π10s
(b) The block of mass 3kg perform SHM with amplitude 4cm
( c) The block of mass 6kg will have maximum momentum of 2.40kg−m/s
(d) The time periods of two blocks are in the ratio of 1:√2
View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View Solution
Knowledge Check
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctIn the arrangements as shown, blocks A and B of the masses as shown move in the direction with velocities as indicated on a smooth surface. The spring constant is 300 N/m. find the maximum compression in the spring (approx).
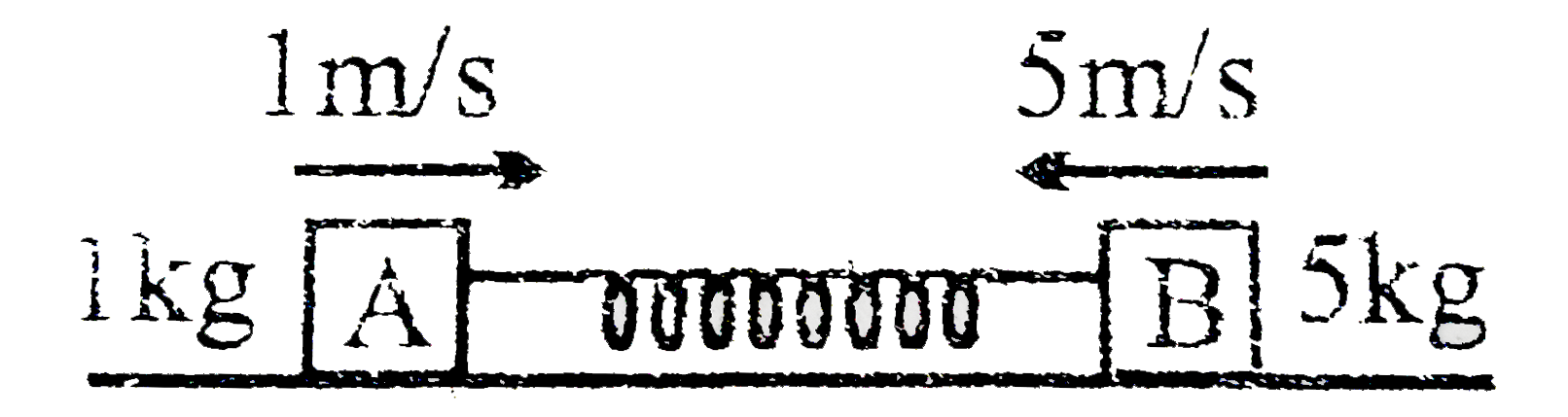 A17 cmB22 cmC32 cmD38 cm
A17 cmB22 cmC32 cmD38 cmA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
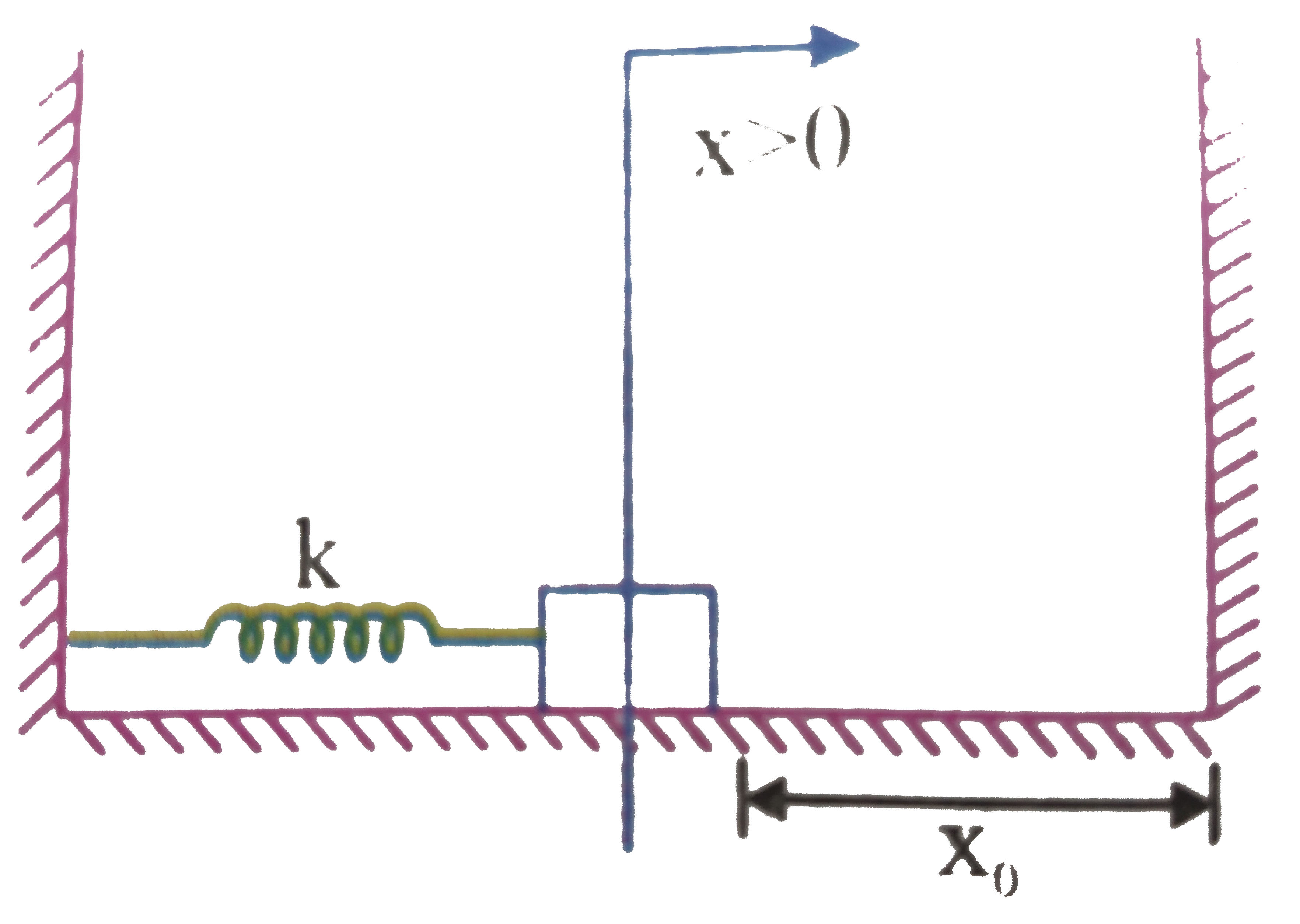
Find the time period of motion of the block:A2π3√mkB4π3√mkC3π2√mkDπ2√mk
For the arrangement shown in figure, the spring is inilially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionFor the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :

View SolutionIn the figure shown, all surfaces are smooth and force constant of spring is 10N/m. Block of mass (2 kg) is attaced with the spring. The spring is compressed by (2m) and then released. Find the maximum distance d travelled by the block over the inclined plane. Take g=10m/s2.
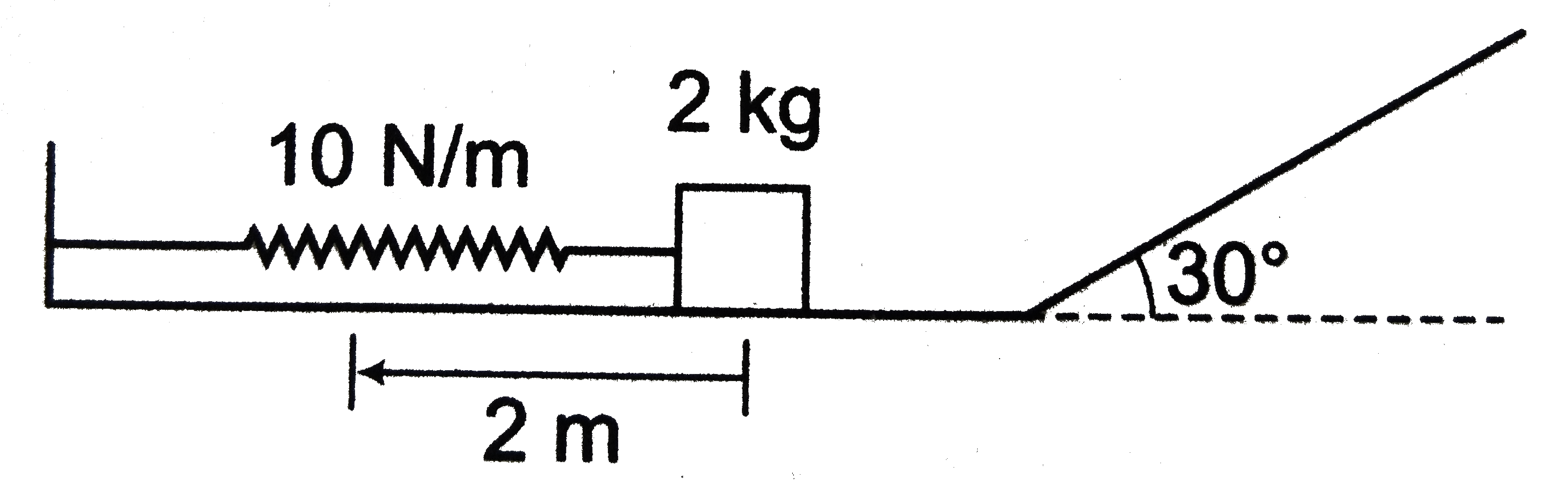 .
.
View SolutionIn the system shown in figure, all surfaces are smooth, pulley and strings are massless. Mass of both A and B are equal. The system is released from rest.

(a) Find the →aA.→aB immediately after the system is released. →aAand→aB are accelerations of block A and B respectively.
(b) Find →aA immediately after the system is released.
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
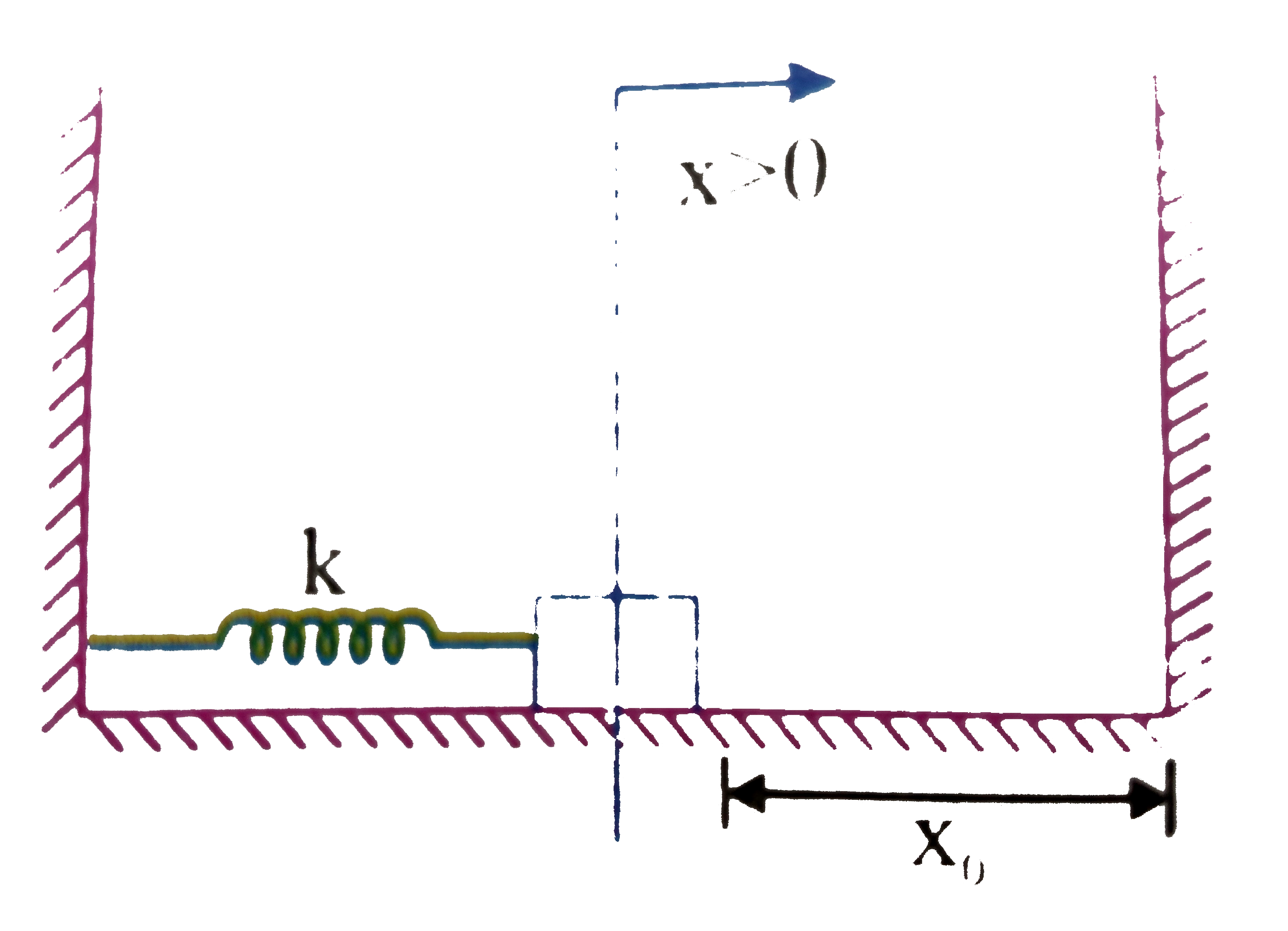
Write its equation of motion indicating position as a function of time:
View Solution

