In an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12×10−15Vs. Given e=1.6×10−19C, estimate the value of Planck's constant.
The slope of the cut-off voltage (V) versus frequency (v) of an incident light is given as : Vv=4.12×10−15Vs
V is related to frequency by the equation : hv=eV
Where, e=Charge on an electron =1.6×10−19C
h=Planck's contant ∴h=e×Vv
=1.6×10−19×4.12×10−15=6.592×10−34Js
Therefore , the value of Planck's constant is 6.592×10−34Js
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise37videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERTCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE23videos
CURRENT ELECTRICITY
- BOOK - NCERTCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE34videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
In an experiment on photoelectric effect, the slope of the cut-offf voltage versus frequency of incident light is found to be 4.12×10−15V s. calculate the value of Planck's constant.
View SolutionIn a photoelectric experiment, it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300nm to 400nm. Calculate the value of the Planck constant from these data.
View Solution
Knowledge Check
- Question 1 - Select One
In an experiment on the photoelectric effect , the slope of the cut - off voltage versus frequency of incident light is found to be 4.12×10−15V s . The value of Planck's constant is
A6.592×10−34 J sB6.592×10−31 J sC9.592×10−34 J sD6.592×10−30 J s - Question 2 - Select One
Photons of frequencies 2.2×1015Hz and 4.6×1015Hz are incident on a metal surface. The corresponding stopping potentials were found to be 6.6V and 16.5V respectively. Given e=1.6×10−19c, the value of universal planck's constant is
A6.6×10−34JsB6.7×10−34JsC6.5×10−34JsD6.8×10−34Js - Question 3 - Select One
In a photoelectric experiment it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300 nm to 400 nm. Calculate the value of the Planck constant from these data.
A4.12×10−15 eVsB2.5×1010eVsC5.2×10−15 eVsD7.5×10−8 eVs
Calculate the speed of the electron in the first Bohr orbit given that h=6.6×10−34Js,m=9.11×10−31kg and e=1.603×10−19C.
View SolutionFor photoelectric effect in sodium, fig. shows the plot of cut-off voltage versus frequency of the incident radiation. Caclculate:
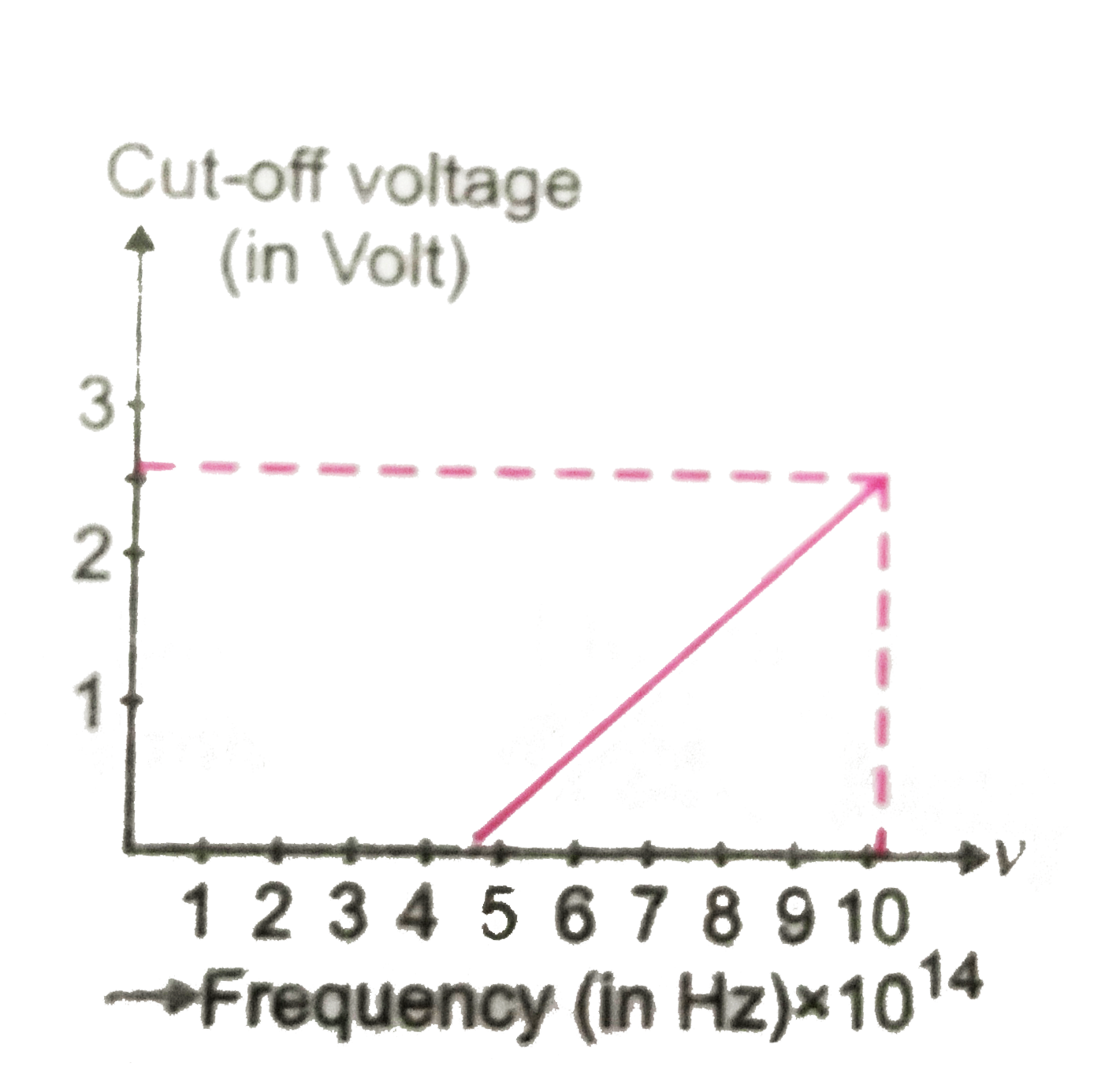
(i) the threshold frequency
(ii) the work function for sodium. (Use h=6.6×10−34Js)View SolutionIn an experiment to measure the charge on an electron, the following values of charge were found on oil droplets: −1.6×10−15,−2.4×10−19,−4.0×10−19 (in coulomb). What values of electronic charge would be indicated by these results?
View SolutionBy how which would the stopping potential for a given photosensitive surface go up if the frequency of the incident radiations were to be increased from 4×1015Hz to 8×1015Hz? Given, h=6.6×10−34Js, e=1.6×10−19Candc=3×108ms−1.
View SolutionElectrons ejected from the surface of a metal, when light of certain frequency is incident on it, are stopped fully by a retarding potential of 3 volts. Photo electric effect in this metallic surface begains at a frequency 6×1014s−1. The frequency of the incident light in s−1 is [h=6x10−34J−sec, charge on the electron =1.6×10−19C]
View Solution