For a given velocity, a projectile has the same range R for two angles of projection. If t1 and t2 are the time of flight in the two cases, then t1t2 is equal to
The correct Answer is:2
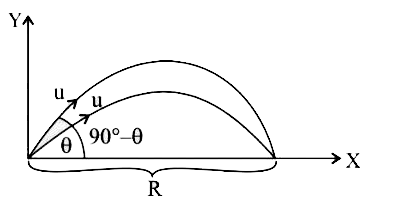
t1=2usinθg, t2=2usin(90∘−θ)g
t1.t2=2usinθg.2usin(90∘−θ)g, t1t2=2×2u2sinθcosθg2
t1t2=2u2g.2sinθcosθg, t1t2=2u2g.sin2θg t1t2=2Rg
Similar Questions
A projectille can have the same rangeR for two angles of projection. If t1 and t_(2)bethetimeofflight∈thetwocases,thenf∈dtherelationbetween t_(1), t_(2)andR .
View SolutionA projectile can have the same range R for two angles of projection .If t1and t2be the times of flight in the two cases, then the product of the two times of fight is directly proportional to
View Solution
Knowledge Check
For a given velocity, a projectile has the same range R for two angles of rpojection if t1 and t2 are the times of flight in the two cases then
At1t2∝R2Bt1t∝RCt1t2∝1RDt1t2∝1R2For a given velocity, a projectile has the same range R for two angles of rpojection if t1 and t2 are the times of flight in the two cases then
At1t2∝RBt1t2∝R2Ct2t2∝1R2Dt1t2∝1RA projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in the two cases:-
At1t2∝R2Bt1t2∝RCt1t2∝1RDt1t2∝1R2
A projectile can have same range R for two angles of projection. It t1andt2 are the times of flight in the two cases, then what is the product of two times of flight ?
View SolutionA projectile can have the same rangeR for two angle of projection . If t−1 and t2 be the terms of flight in the two cased then the initial velocity of projectile is?
View SolutionA projectile has the same range R for two angles of projections but same speed. If T1 and T2 be the times of flight in the two cases, then
Here θ is the angle of projection corresponding to T1.
View SolutionA projectile has the same range R for angles of projections. If T1andT2 be the times of fight in the two cases, then ( using θ as the angle of projection corresponding to T1 )
View SolutionA projectile can have the same range 'R' for two angles of projection . If 'T1' and 'T2' to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
View Solution
