There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its intantanradius R(t) is :
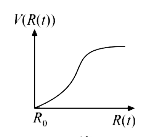
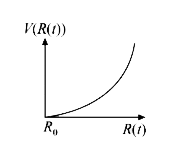
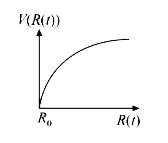

The correct Answer is:C
No net external force on system Hence Total Energy will be conserved.
Ui+Ki=Uf+Kf
KQ22r0+0=KQ22r+1rmv2.
v=√KQ2m(1r0−1r)
Quadratic concave down .
Similar Questions
There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is initially at rest and starts expanding because of mutual repulsion , the figure that represents best the speed V (r(t)) of the distribution as a function of its instant radius R(t) is :
View SolutionFor a spherically symmetrical charge distribution electric field at a distance r from the centre of sphere is →E=kr2ˆr where k is a constant what will be the volume charge density at a distance r from the centre of sphere?
View Solution
Knowledge Check
For spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
Aρ=9kε0r6Bρ=5kε0r3Cρ=3kε0r6Dρ=9kε0r0The maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
A√σmε0tRB√2σmε0tRC√3σmε0tRD√4σmε0tRA large plate with uniform surface charge density σ is moving with constant speed v as shown in the figure. The magnetic field at a small distance from plate is
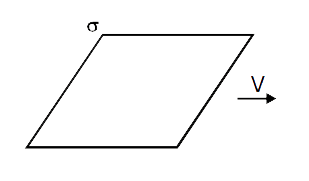 Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plate
Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plate
The energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.
View SolutionConsider a uniform charged sphere of charge density r and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure. If the electric field at the centre of the cavity is (rho R)/(n varepsilon_(0)find n .
View SolutionA sphere of radius R_(0 carries a volume charge density proportional to the distance (x) from the origin, rho=alpha x where alpha is a positive constant.The total charge in the sphere of radius R_(0) is
View Solution7.Consider a uniform charged sphere of charge density p and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure.If the electric field at the centre of the cavity is ρRnɛ0find n .
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution
