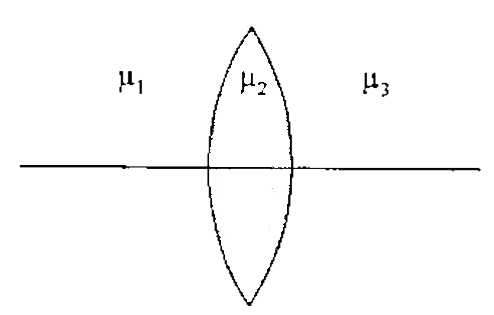
A plano convex lens of refractive index μ1 and focal length f1 is kept in contact with another plano concave lens of refractive index μ2 and focal length f2. If the radius of curvature of their spherical faces is R each and f1=2f2, then μ1 and μ2 are related as :
μ1+μ2=3
3μ2−2μ1=1
2μ2−μ1=1
2μ1−μ2=1
The correct Answer is:D
1f1=(μ1−1)(1R−1∞)
⇒f1=Rμ1−1
1f2=(μ2−1)(1∞−1R)=1−μ2R
⇒f2=R1−μ2
|f1|=2|f2|⇒Rμ1−1=2Rμ2−1⇒μ2−1=2μ1−2⇒2μ1−μ2=1
Similar Questions
Knowledge Check
A Plane convex lens of refractive index μ1 and focal length f1 is kept in contact with another plane concave lens of refractive index μ2 and focal length f2 If the radius of curvature of their spherical faces is R each and f1=3f2 then μ1 and μ2 are related as:
Aμ1+μ2=3B3μ1−2μ1=1C3μ2−μ1=1D3μ1−μ2=2A plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
A400 cmB200 cmC100 cmD50 cmA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
A50 cmB100 cmC200 cmD150 cm
A plano-convex lens μ=1.5 has focal length of 18 cm in air. Calculate the radius of curvature of the spherical surface.
View SolutionA convex lens of focal length f1 is kept in contact with another lens of focal length/2. Find an expression for the focal length of the combination.
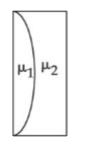
View SolutionCurved surfaces of a plano-convex lens of refractive index μ1 and a plano-concave lens of refractive index μ2 have equal radius of curvature as shown in figure. Find the ratio of radius of curvature to the focal length of the combined lenses.
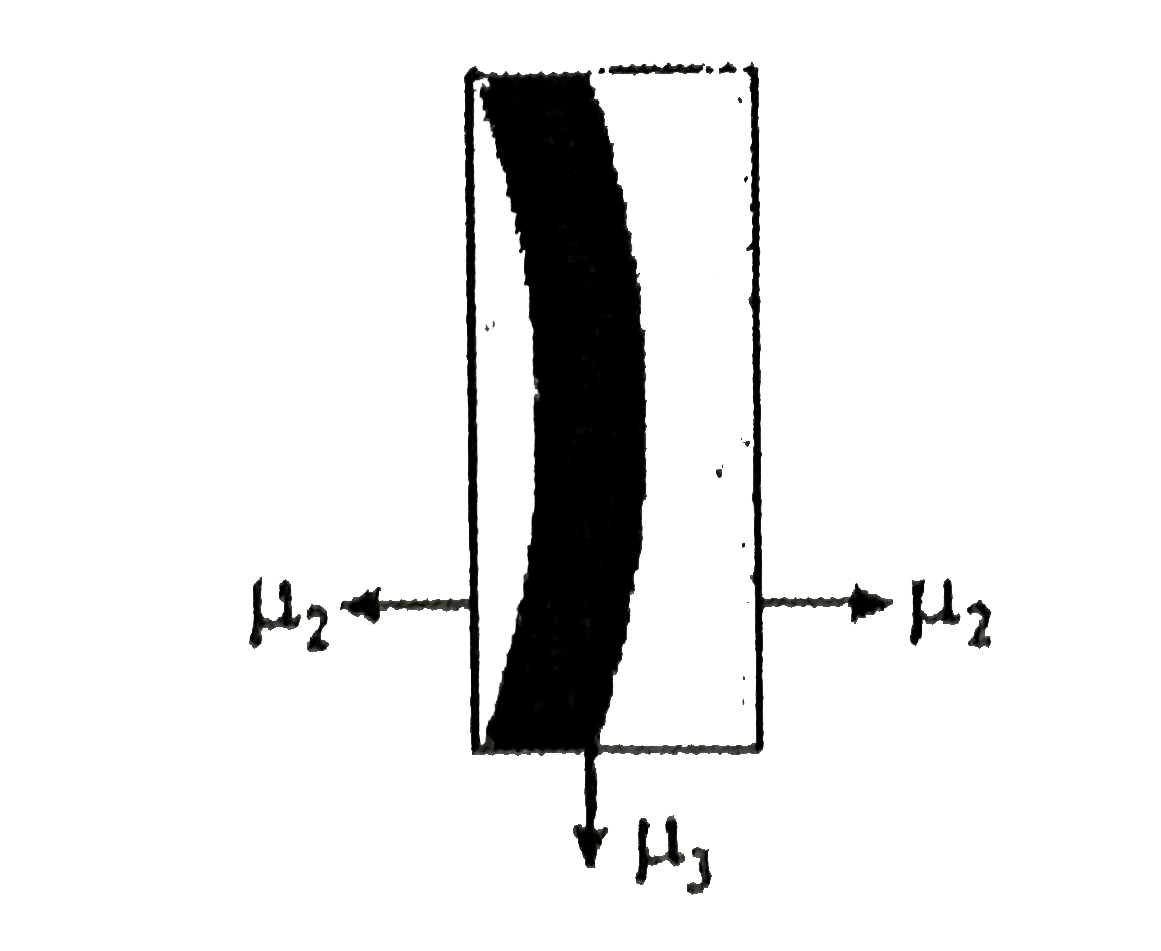
View SolutionThe figure below shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. Another thin lens of refractive index μ3 has same radius of curvature R on the two surface between the plano-convex and plano-concae lenses that the plane surfaces are parallel to each other. Find the focal length of the combination.
View SolutionConsider an equiconvex lens of radius of curvature R and focal length f. If f>R , the refractive index μ of the material of the lens
View Solution