In a double star, two stars (one of mass $m$ and the other of mass $2 m$ ) distance $d$ apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.

Video Solution

Text Solution

Verified by Experts

The centre of mass of double star from mass $m_{1}$ is given by
$r_{c m} = \frac{m_{1} r_{1} + m_{2} r_{2}}{m_{1} + m_{2}} = \frac{m_{1} \times 0 + m_{2} d}{m_{1} + m_{2}} = \frac{m_{2} d}{m_{1} + m_{2}}$
$∴$ Distance of centre of mass from $m_{2}$ is

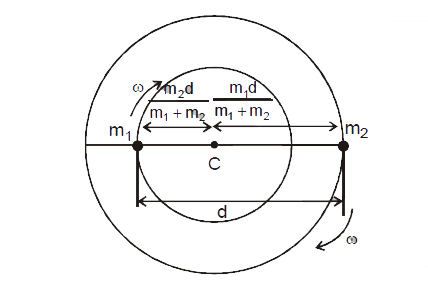
$r'_{c m} = d - r_{c m} = d - \frac{m_{2} d}{m_{1} + m_{2}} = \frac{m_{1} d}{m_{1} + m_{2}}$
Both the stars rotate around centre of mass in their own circular orbits with the same angular speed $ω$ . the gravitational force acting on each star provides the necessary centripetal force. if we consider the rotation of mass $m_{1}$ , then
$m_{1} (r_{c m}) ω^{2} = \frac{G m_{1} m_{2}}{d^{2}}$
or $m_{1} (\frac{m_{2} d}{m_{1} + m_{2}}) ω^{2} = \frac{G m_{1} m_{2}}{d^{2}}$
This give $ω = \frac{2 π}{T} = \sqrt{(\frac{G (m_{1} + m_{2})}{d^{3}})}$
or Period of revolution
$T = 2 π \sqrt{(\frac{d^{3}}{G (m_{1} + m_{2})})}$
Ratio of Angular Momenta is
$\frac{J_{1}}{J_{2}} = \frac{I_{1} ω}{I_{2} ω} = \frac{I_{1}}{I_{2}} = \frac{{(m_{1} \frac{m_{2} d}{m_{1} + m_{2}})}_{1}^{2}}{m_{2} {(\frac{m_{1} d}{m_{1} + m_{2}})}^{2}} = \frac{m_{2}}{m_{1}}$
Ratio of kinetic energies is
$\frac{K_{1}}{K_{2}} = \frac{\frac{1}{2} I_{1} ω^{2}}{\frac{1}{2} I_{2} ω^{2}} = \frac{I_{1}}{I_{2}} = \frac{m_{2}}{m_{1}}$

Updated on:21/07/2023