Points B and C lie on ¯¯¯¯¯¯AD as shown below. The length of ¯¯¯¯¯¯AD is 30 units, ¯¯¯¯¯¯AC is 16 units long, and ¯¯¯¯¯¯BD is 20 units long. How many units long, if it can be determined, is ¯¯¯¯¯¯BC ?
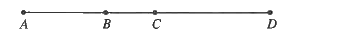
4
6
10
14
The correct Answer is:B
Step by step video, text & image solution for Points B and C lie on bar(AD) as shown below. The length of bar(AD) is 30 units, bar(AC) is 16 units long, and bar(BD) is 20 units long. How many units long, if it can be determined, is bar(BC) ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
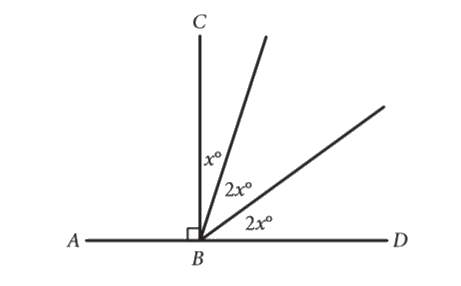
In the figure above, point B lies on ¯¯¯¯¯¯AD . What is the value of 3x ?
View SolutionParallelogram ABCD is graphed in the standard (x,y) coordinate plane below. Sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD are each √10 coordinate units long. Sides ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC are each 5 coordinate unit long. The distance between ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC is 3 coordinate units.
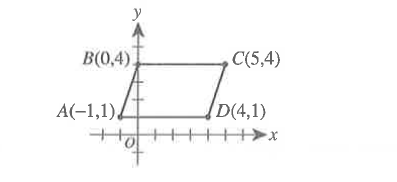
What is the area, in square coordinate units, of ABCD ?
View Solution
Knowledge Check
In the figure below, ¯¯¯¯¯¯AB≡¯¯¯¯¯¯ACand¯¯¯¯¯¯BC is 10 units long. What is the area, in square in square inches, of △ABC ?
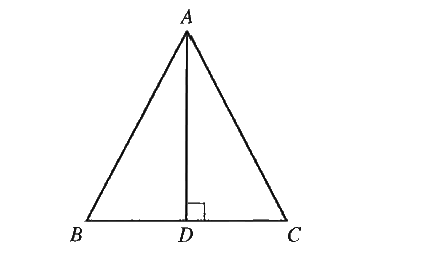 A12.5B25C25√2DCannot be determined from the given information
A12.5B25C25√2DCannot be determined from the given informationPoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
A1B2C3D4Parallelogram ABCD is graphed in the standard (x,y) coordinate plane below. Sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD are each √10 coordinate units long. Sides ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC are each 5 coordinate unit long. The distance between ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC is 3 coordinate units.
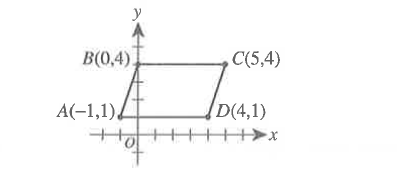
What is the distance, in coordinate units, from B to D?A3B4C5D7
Parallelogram ABCD is graphed in the standard (x,y) coordinate plane below. Sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD are each √10 coordinate units long. Sides ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC are each 5 coordinate unit long. The distance between ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC is 3 coordinate units.

What is the slope of BC↔?
View SolutionParallelogram ABCD is graphed in the standard (x,y) coordinate plane below. Sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD are each √10 coordinate units long. Sides ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC are each 5 coordinate unit long. The distance between ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC is 3 coordinate units.
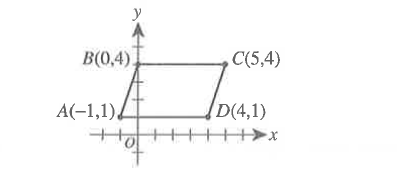
Parallelogram ABCD will be reflected over the y-axis. what will be the coordinates of the image of A?
View SolutionIn the circle with center D shown below, the length of radius ¯¯¯¯¯¯CD is 4 cm, the length of ¯¯¯¯¯¯BC is 1 cm, and ¯¯¯¯¯¯BC is perpendicular to radius ¯¯¯¯¯¯AD at B. When ∠ADC is measured in degree, which of the following expressions represents the length, in centimeters, of ¯¯¯¯¯¯AC?
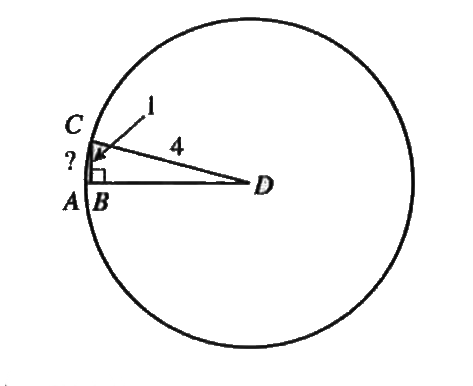
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
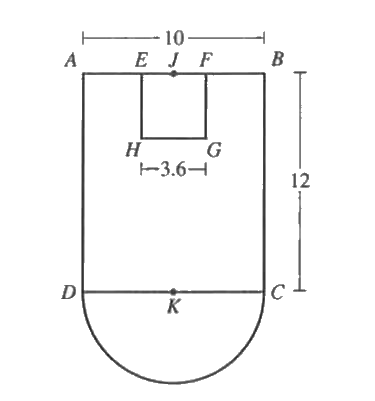
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
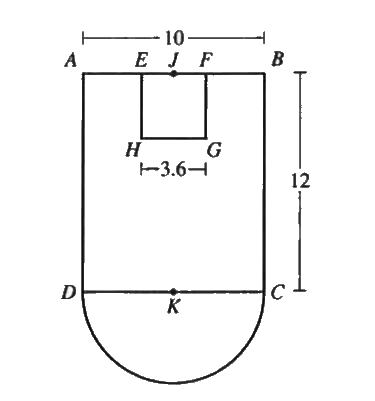
What is the length, in meters, of ¯¯¯¯¯¯JD?
View Solution
