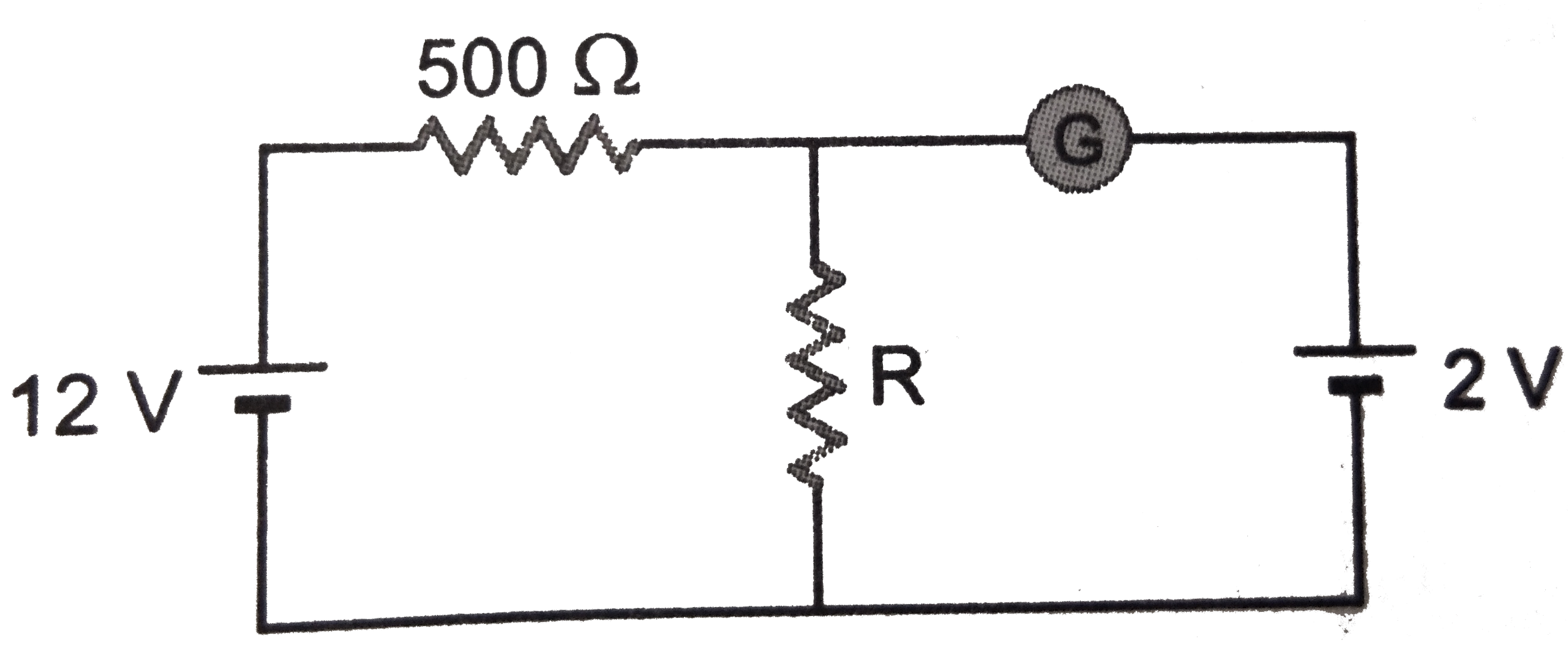
For the circuit, the galvanometer G shows zero deflection. If the batteries A and B have negligible internal resistance, the value of the resistor R will be
200Ω
100Ω
500Ω
1000Ω
The correct Answer is:B
To solve the problem, we need to analyze the circuit and apply the principles of current electricity. The key point here is that the galvanometer shows zero deflection, indicating that no current flows through it. This means that the potential difference across the galvanometer is zero, and we can use this information to find the value of the resistor R.
1. Understanding Zero Deflection:
- When the galvanometer shows zero deflection, it indicates that the current through it is zero. This means that the potential difference across the galvanometer is equal to zero.
2. Analyzing the Circuit:
- Let's denote the voltage of battery A as VA=12V and the voltage of battery B as VB=2V.
- The galvanometer is connected in such a way that the two batteries are in two different branches of the circuit.
3. Applying Kirchhoff's Voltage Law:
- Since there is no current flowing through the galvanometer, we can analyze the two loops formed by the batteries and resistors.
- For the loop containing battery A and resistor R:
VA=I⋅(500Ω+R)
- Since I=0 (no current through the galvanometer), we can set up the equation as:
12=0⋅(500+R)(not useful since current is zero)
4. Voltage Across Resistor R:
- The voltage across resistor R can be expressed as:
VR=IR⋅R
- Since the current through R is also zero, we need to consider the voltage across the other branch (with battery B):
VB=IB⋅500Ω
- Since the galvanometer shows zero deflection, the voltage across the galvanometer must equal the voltage across R.
5. Setting Up the Equation:
- The voltage across R must equal the voltage across the 500-ohm resistor:
2=12500+R⋅R
6. Cross Multiplying:
- Rearranging gives:
2(500+R)=12R
- Expanding this:
1000+2R=12R
7. Solving for R:
- Rearranging the equation:
12R−2R=1000
10R=1000
R=100010=100Ω
Final Answer:
The value of the resistor R is 100Ω.
- When the galvanometer shows zero deflection, it indicates that the current through it is zero. This means that the potential difference across the galvanometer is equal to zero.
- Let's denote the voltage of battery A as VA=12V and the voltage of battery B as VB=2V.
- The galvanometer is connected in such a way that the two batteries are in two different branches of the circuit.
- Since there is no current flowing through the galvanometer, we can analyze the two loops formed by the batteries and resistors.
- For the loop containing battery A and resistor R:
VA=I⋅(500Ω+R)
- Since I=0 (no current through the galvanometer), we can set up the equation as:
12=0⋅(500+R)(not useful since current is zero)
- The voltage across resistor R can be expressed as:
VR=IR⋅R
- Since the current through R is also zero, we need to consider the voltage across the other branch (with battery B):
VB=IB⋅500Ω
- Since the galvanometer shows zero deflection, the voltage across the galvanometer must equal the voltage across R.
- The voltage across R must equal the voltage across the 500-ohm resistor:
2=12500+R⋅R
- Rearranging gives:
2(500+R)=12R
- Expanding this:
1000+2R=12R
- Rearranging the equation:
12R−2R=1000
10R=1000
R=100010=100Ω
The value of the resistor R is 100Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:BITSAT GUIDEChapter:CURRENT ELECTRICITYExercise:Bitsat Archives
Explore 26 Videos
- CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSBook:BITSAT GUIDEChapter:CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSExercise:BITSAT Archives
Explore 6 Videos
- ELECTRIC CAPACITORBook:BITSAT GUIDEChapter:ELECTRIC CAPACITORExercise:BITSAT archives
Explore 6 Videos
Similar Questions
Knowledge Check
In the circuit, the galvanometer G shows zero deflection. If the batteries A and B have negligible internal resistance, the value of the resistor R will be
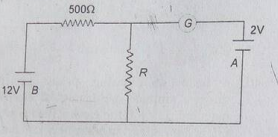 A200ΩB100ΩC500ΩD1000Ω
A200ΩB100ΩC500ΩD1000ΩIn the circuit, the galvanometer G shows zero deflection. If the batteries A and B have negligible internal resistance, the value of the resistor R will be
 A200ΩB100ΩC500ΩD1000Ω
A200ΩB100ΩC500ΩD1000ΩIn the circuit, the galvanometer G shows zero deflection. If the batteries A and b have negligible internal resistance, the value of the resistor R will be -
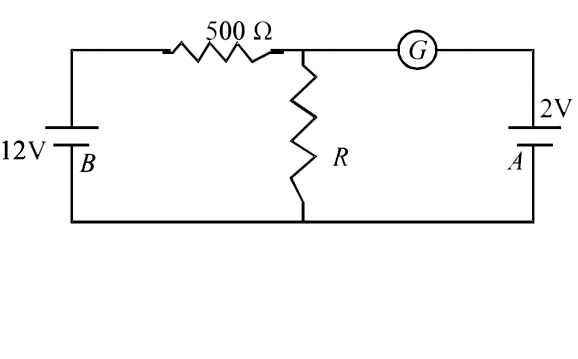 A100ΩB200ΩC1000ΩD500Ω
A100ΩB200ΩC1000ΩD500Ω
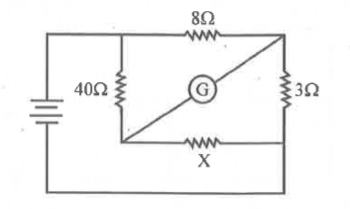
In the given circuit, the galvanometer G gives zero deflection. What is the value of resistance X ?
View SolutionFor the following diagram the galvanometer shows zero deflection then what is the value of R?
View Solution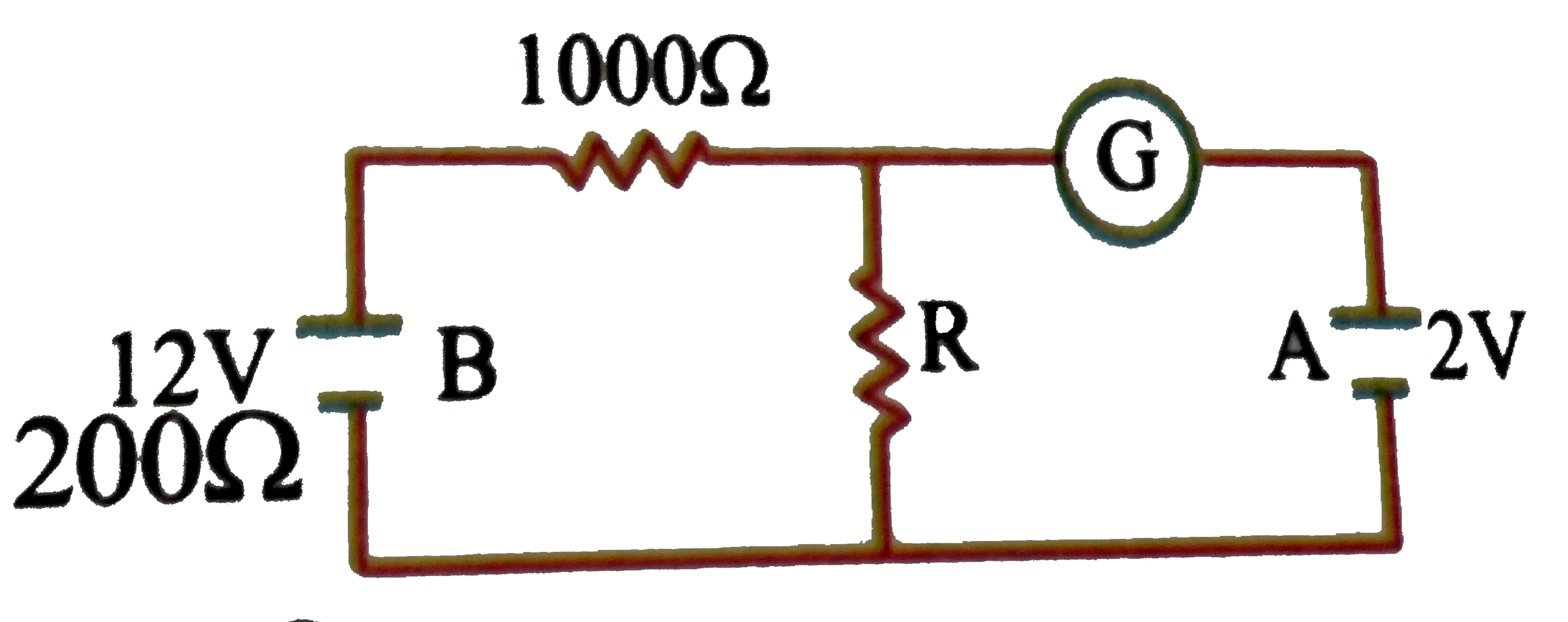
In the circuit the galvanometer G shows zero deflection. If the betteries A and B have negligible internal resistance, the value of the resistor R will be:
View SolutionIn the given circuit, the galvanmeter G will show zero deflection if

View SolutionIn the circuit shown, the galvanometer shows zero current. The value of resistance R is :
View Solution