A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3.Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
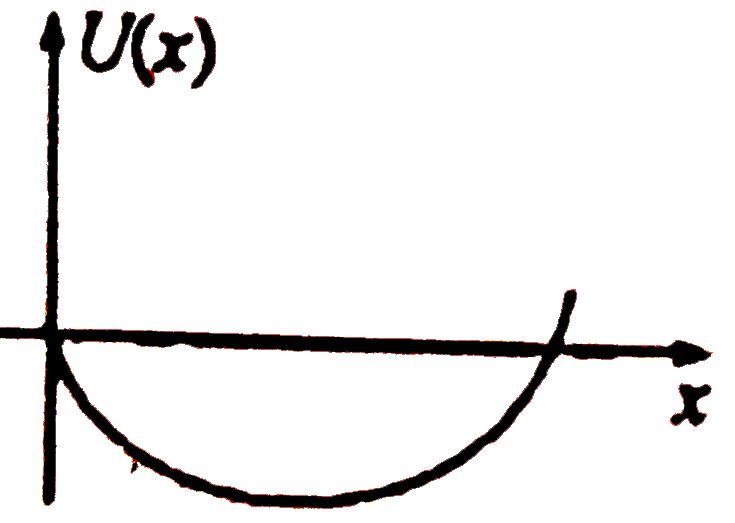
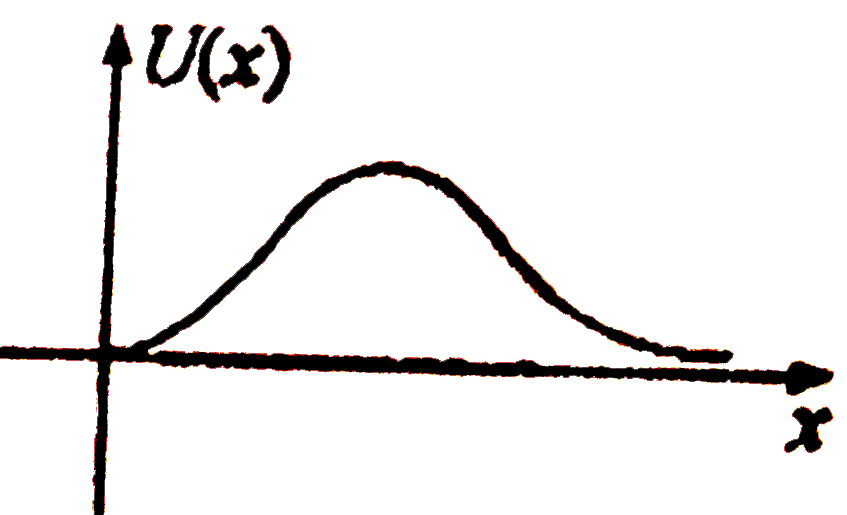
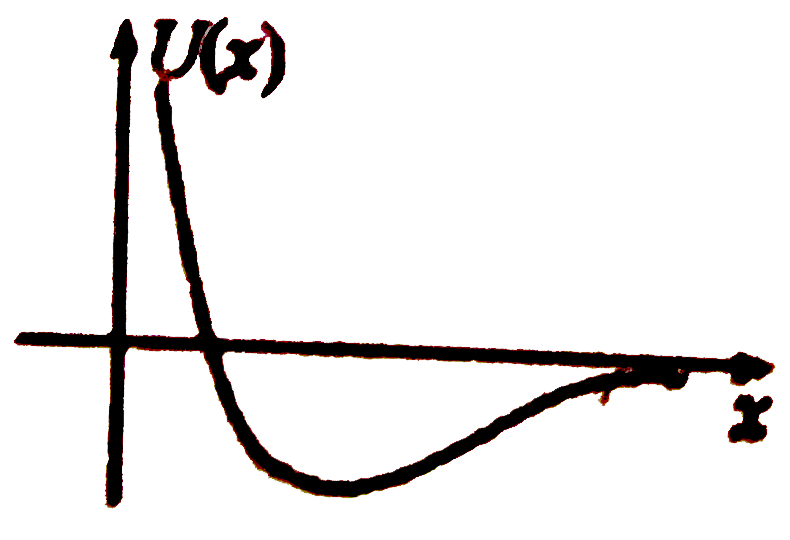
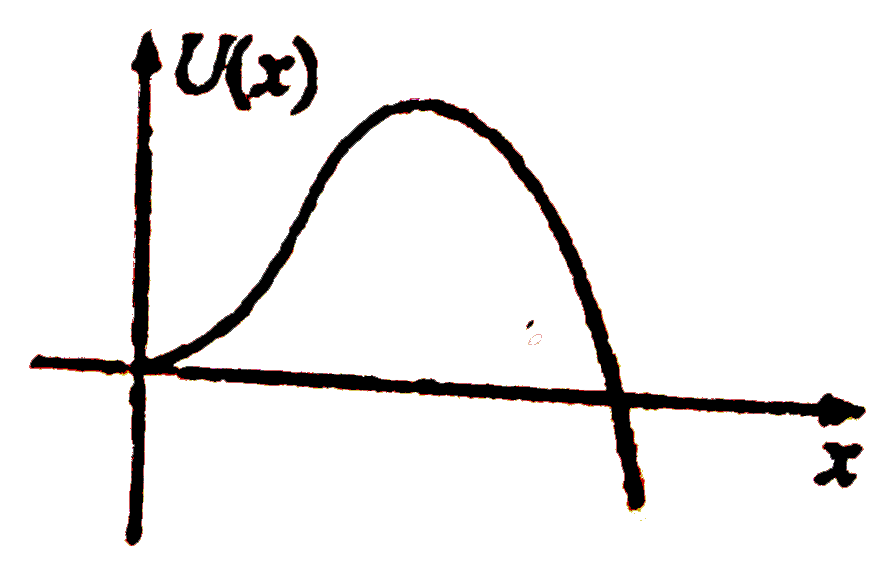
The correct Answer is:D
Step by step video, text & image solution for A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x) = -kx + ax^(3).Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolvedMCQ
78 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question
31 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a)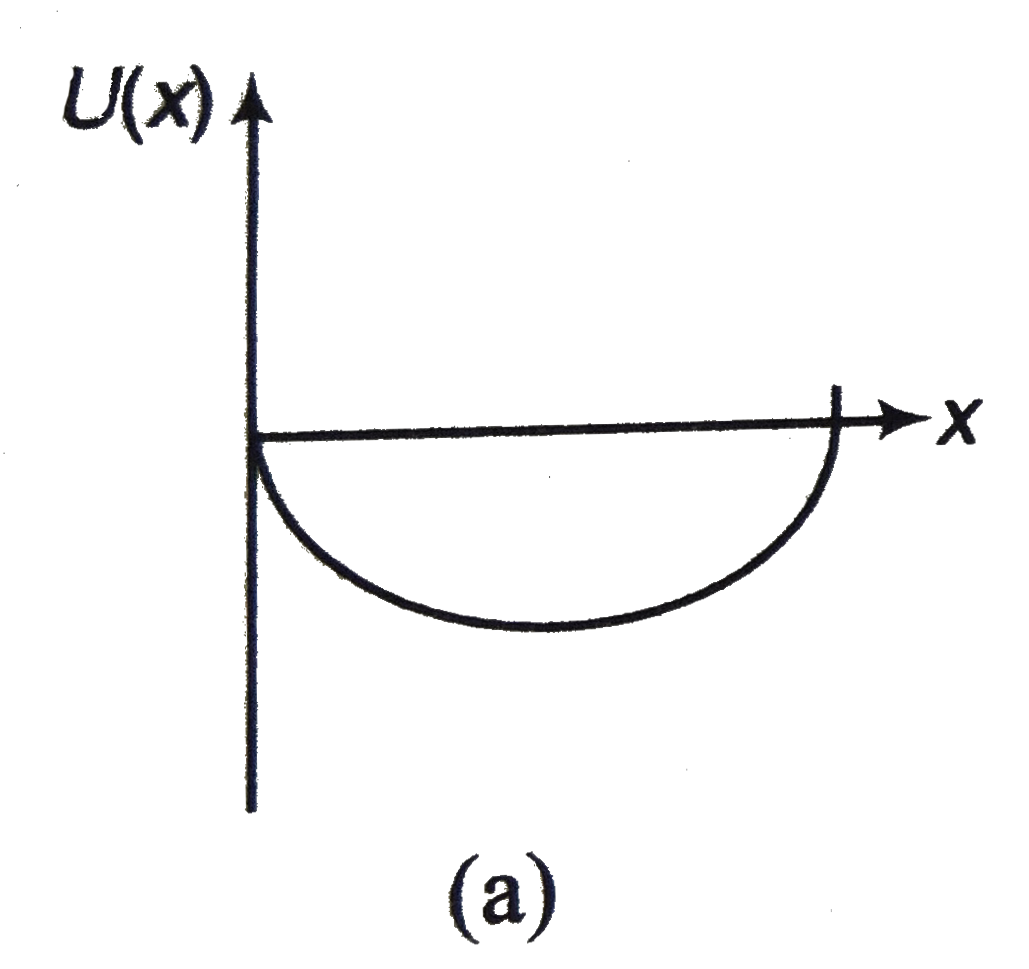 , (b)
, (b) 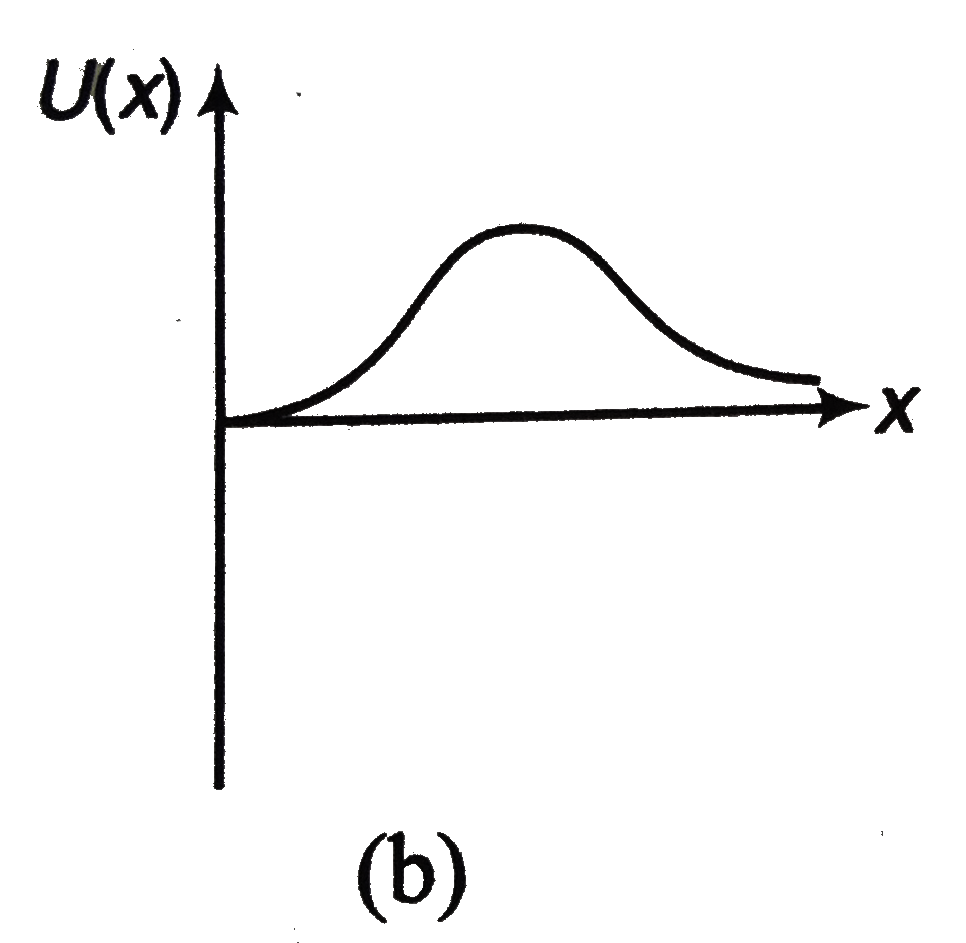 , (c)
, (c) 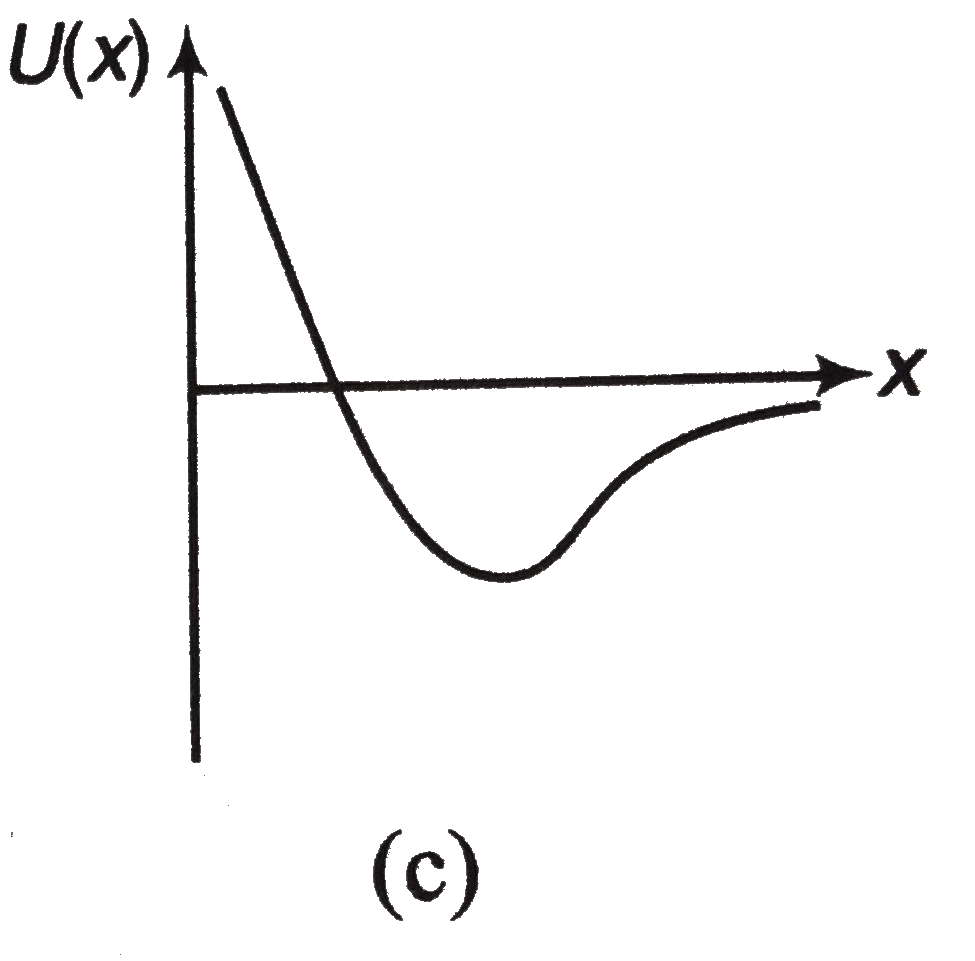 , (d)
, (d) 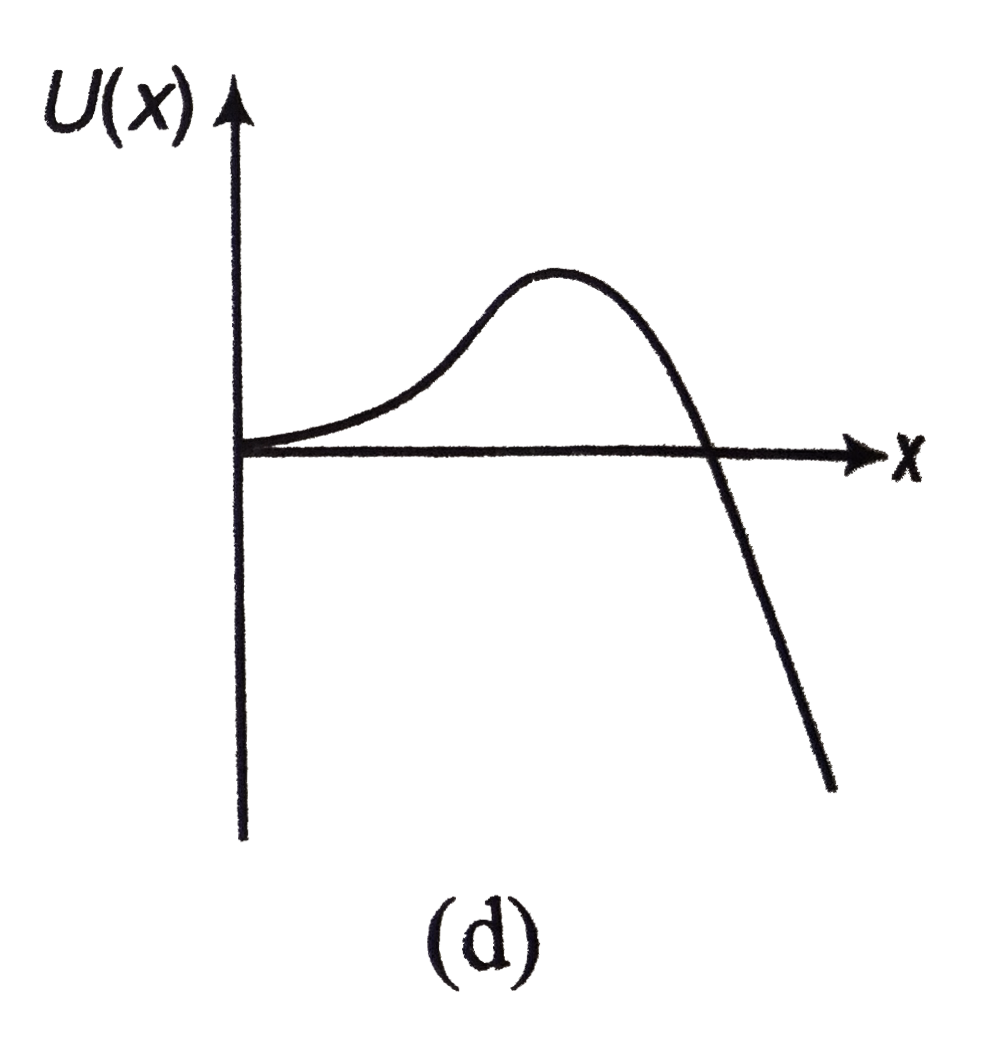 .
.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View Solution
Knowledge Check
A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A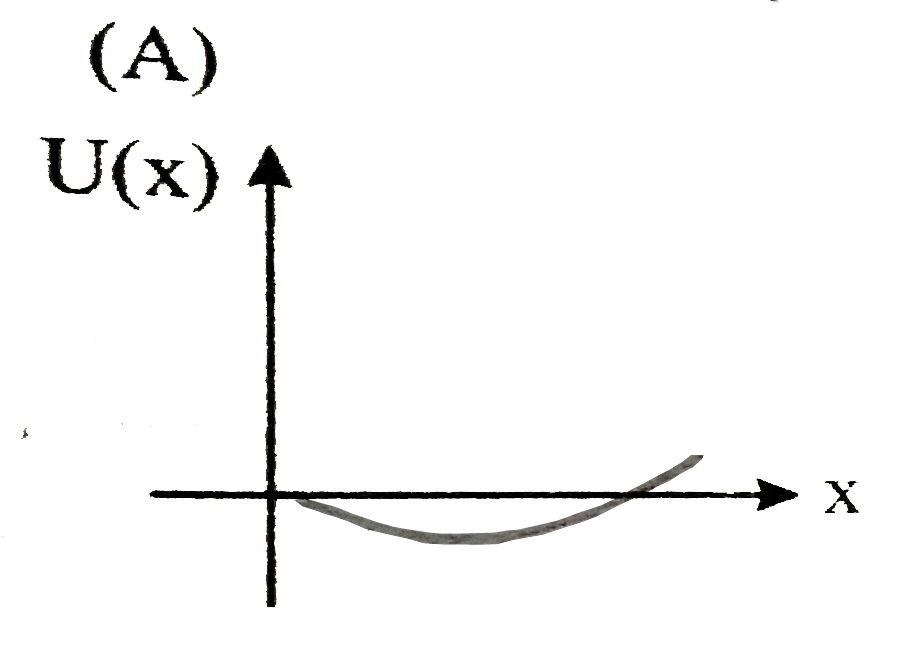 B
B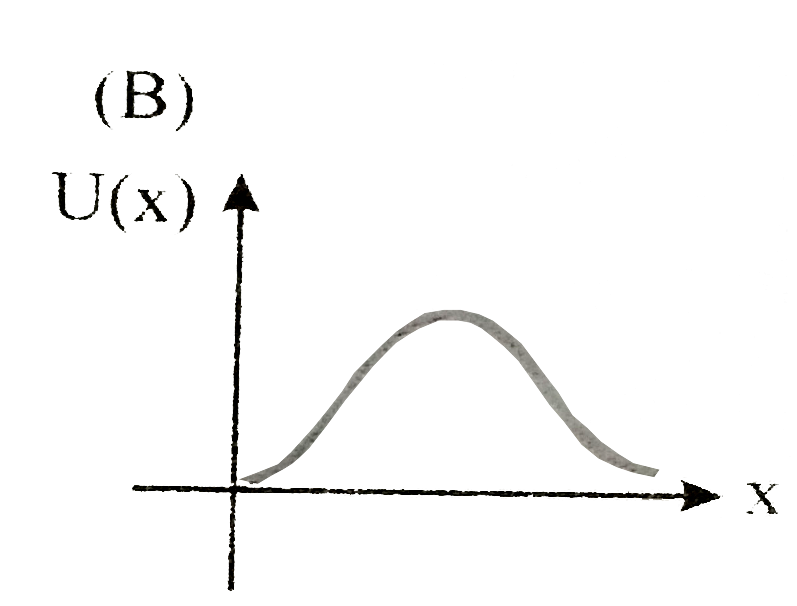 C
C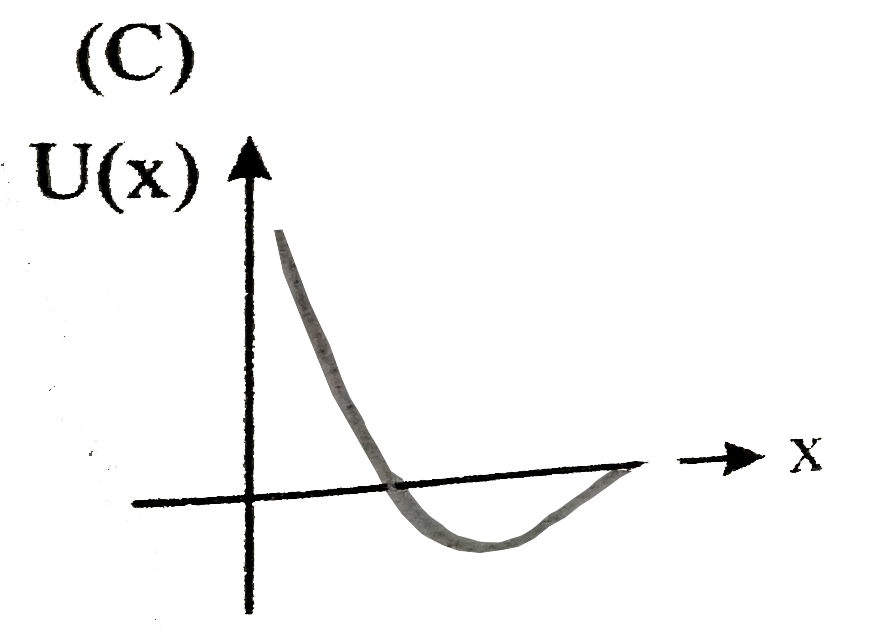 D
D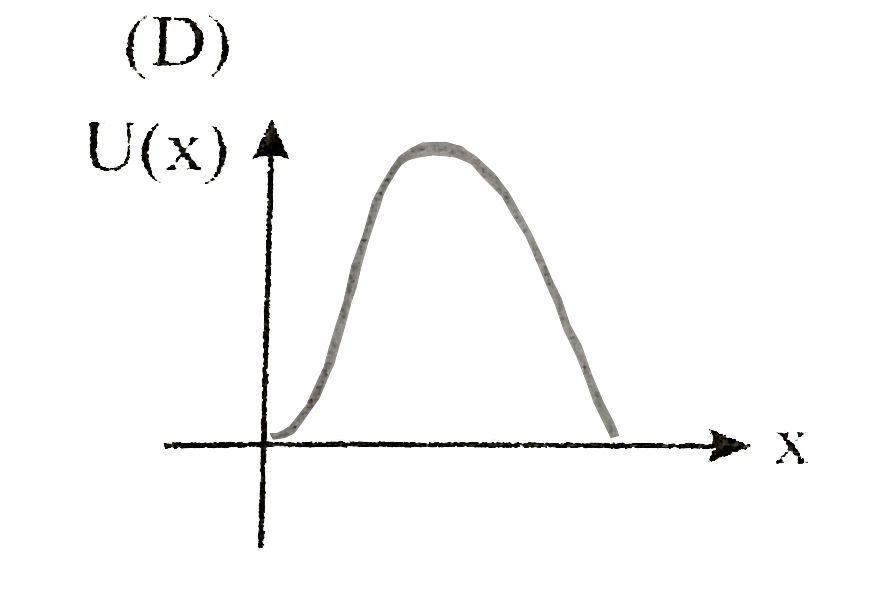
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B C
C D
D
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B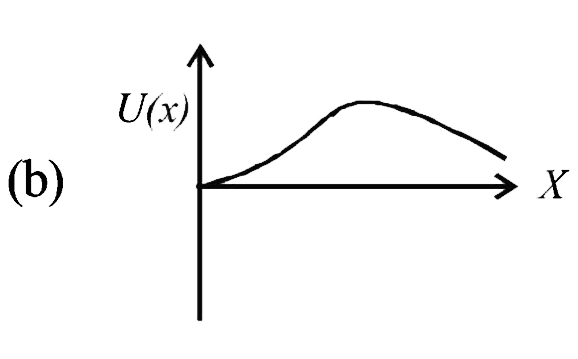 C
C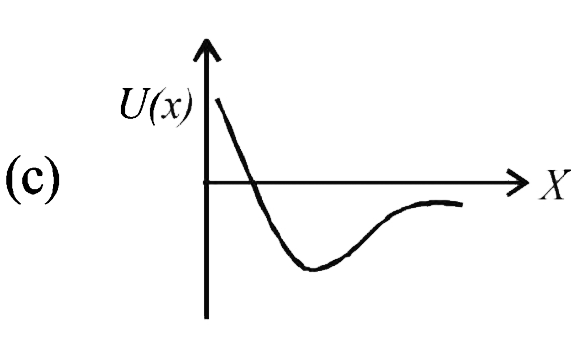 D
D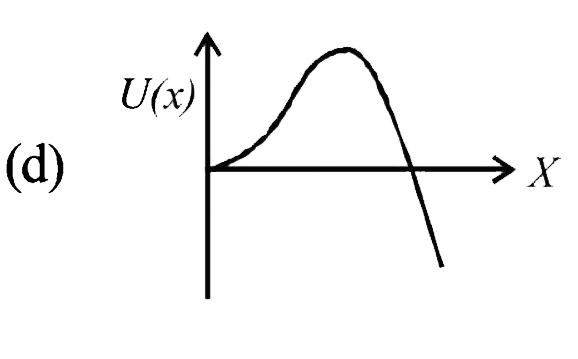
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1/2)kx2 for x<0 and U=0 for x≥0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=−√2E/k is
View Solution
