In (not shown), . If , then what is the area of , in terms of x?
The correct Answer is:A
To find the area of triangle ABC in terms of x, we can follow these steps:
Step 1: Identify the triangle properties
Given:
- ∠ABC=60∘
- AC⊥BC (which means AC is the height and BC is the base of the triangle)
- AB=x
Step 2: Determine the angles of the triangle
Since the sum of angles in a triangle is 180∘:
∠A+∠B+∠C=180∘
Given ∠B=60∘ and ∠C=90∘ (because AC⊥BC):
∠A+60∘+90∘=180∘
∠A=30∘
Step 3: Use trigonometric ratios to find AC and BC
Using the sine and cosine functions:
1. For AC:
sin(60∘)=ACAB⟹√32=ACx
Rearranging gives:
AC=x⋅√32=√3x2
2. For BC:
cos(60∘)=BCAB⟹12=BCx
Rearranging gives:
BC=x⋅12=x2
Step 4: Calculate the area of triangle ABC
The area A of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, BC is the base and AC is the height:
Area=12×BC×AC=12×x2×√3x2
Simplifying this:
Area=12×x2×√3x2=√3x28
Final Answer
Thus, the area of triangle ABC in terms of x is:
Area=√3x28
---
Given:
- ∠ABC=60∘
- AC⊥BC (which means AC is the height and BC is the base of the triangle)
- AB=x
Since the sum of angles in a triangle is 180∘:
∠A+∠B+∠C=180∘
Given ∠B=60∘ and ∠C=90∘ (because AC⊥BC):
∠A+60∘+90∘=180∘
∠A=30∘
Using the sine and cosine functions:
1. For AC:
sin(60∘)=ACAB⟹√32=ACx
Rearranging gives:
AC=x⋅√32=√3x2
cos(60∘)=BCAB⟹12=BCx
Rearranging gives:
BC=x⋅12=x2
The area A of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, BC is the base and AC is the height:
Area=12×BC×AC=12×x2×√3x2
Simplifying this:
Area=12×x2×√3x2=√3x28
Thus, the area of triangle ABC in terms of x is:
Area=√3x28
Topper's Solved these Questions
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:Geometry Drill 2: Calculator-Permitted Section
Explore 8 Videos
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:EXAMPLES
Explore 13 Videos
- FUNCTIONS AND GRAPHSBook:PRINCETONChapter:FUNCTIONS AND GRAPHSExercise:Functions and Graphs Drill 2: Calculator -Permitted Section
Explore 6 Videos
- GRID-INSBook:PRINCETONChapter:GRID-INSExercise:Grid-In Drill 2: Calculator-Permitted Section
Explore 6 Videos
Similar Questions
Knowledge Check
In △ABC (not shown), AC⊥BCadcos∠ABC=1213. What is the value of tan∠ABC?
A513B512C1213D125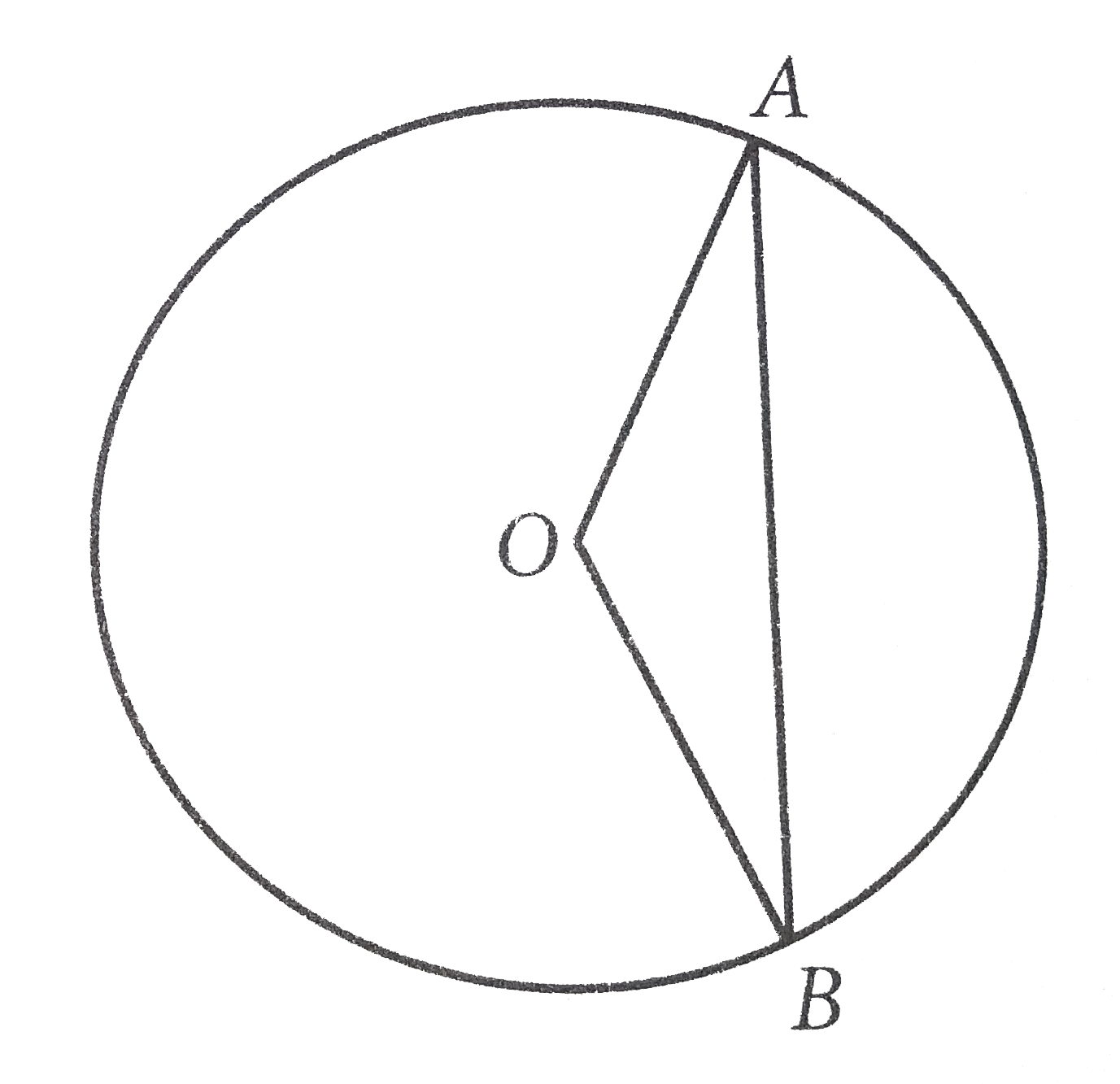
If the radius of the circle above is x, ∠AOB=120∘, and O is the center of the circle, what is the length of chord AB, in terms of x?A√2xB√3xCx√2Dx√3If x+3x−3=y , what is the value of x in terms of y?
A3−yB3/yC√y+12D−3y−31−y
If in △ABC,a=2√3,b=3√2 and ∠B=60∘, then find the measure of ∠C.
View SolutionIn △ABC,∠A=60∘ prove that BC2=AB2+AC2−AB.AC
View SolutionIn ΔABC,AB=AC=x,BC=10cm and the area of triangle is 60 cm2. Find x.
View SolutionIn triangle ABC , ∠ABC=90∘,∠CAB=x∘,tanx∘=34andBC=15cm. Find the measures of AB and AC.
View SolutionGiven, the angles A, B and C of △ABC. Let M be the mid-point of segment AB and let D be the foot of the bisector of ∠C. Find the ratio of AreaOf△CDMAreaof△ABC
View Solution

