The circular orbit of two satellites have radii r1 and r2 respectively (r1<r2). If angular velosities of satellites are same, then their centripetal accelerations are related as
a1>a2
a1=a2
a1<a2
Data insufficient
The correct Answer is:C
To solve the problem, we need to relate the centripetal accelerations of two satellites in circular orbits with different radii but the same angular velocity. Let's denote the centripetal accelerations of the satellites as A1 for the satellite with radius r1 and A2 for the satellite with radius r2.
1. Understanding Centripetal Acceleration:
The centripetal acceleration A of an object moving in a circular path can be expressed in terms of its angular velocity ω and the radius r of the circular path:
A=ω2r
2. Applying the Formula to Both Satellites:
For the first satellite with radius r1:
A1=ω2r1
For the second satellite with radius r2:
A2=ω2r2
3. Comparing the Two Accelerations:
Since we know that r2>r1 and both satellites have the same angular velocity ω, we can compare the two expressions:
A1=ω2r1andA2=ω2r2
4. Establishing the Relationship:
Since r2>r1, we can conclude:
A2=ω2r2>ω2r1=A1
Therefore, we have:
A2>A1
5. Final Conclusion:
The centripetal acceleration of the satellite with the larger radius r2 is greater than that of the satellite with the smaller radius r1:
A2>A1
The centripetal acceleration A of an object moving in a circular path can be expressed in terms of its angular velocity ω and the radius r of the circular path:
A=ω2r
For the first satellite with radius r1:
A1=ω2r1
For the second satellite with radius r2:
A2=ω2r2
Since we know that r2>r1 and both satellites have the same angular velocity ω, we can compare the two expressions:
A1=ω2r1andA2=ω2r2
Since r2>r1, we can conclude:
A2=ω2r2>ω2r1=A1
Therefore, we have:
A2>A1
The centripetal acceleration of the satellite with the larger radius r2 is greater than that of the satellite with the smaller radius r1:
A2>A1
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together
67 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Two wires of same material and same length have radii r1andr2 respectively. Compare their resistances.
View SolutionTwo cars of masses m1 and m2 are moving in circles of raddii r1 and r2 respectively. Their speeds are such that they make complete circle in the same time t The ratio of their centripetal acceleration is .
View Solution
Knowledge Check
Two bodies of masses 8 kg and 4 kg are moving in concentric circular orbits of radii r1andr2 respectively . If their time periods are same , the ration of their centripetal accelerations is
Ar1:r2B2r1:r2Cr1:2r2Dr1:r2The radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
A3v/4B6vC12vD3v/2Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If the two have same massAA would have more potential energy than B while on their B while on their initial circular paths.BA would have more kinetic energy than B while on their initial circular paths.CRelative to Earth's centre, angular momentume of A when it is in elliptical path would be less than angular momentum of B.DDuring the whole process angular of B T than taken by A in moving from position 1 to position 2
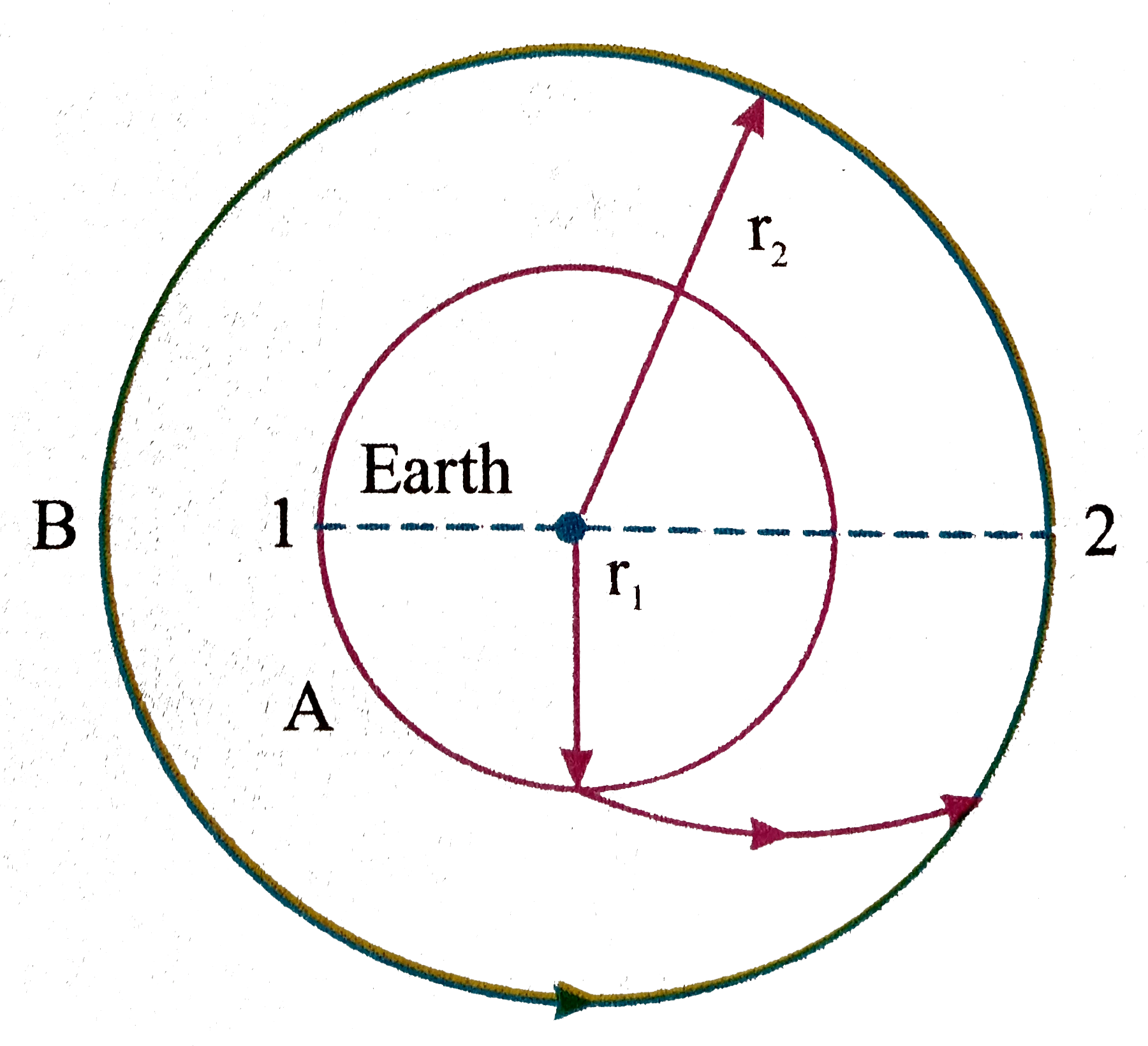
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T then time taken by A in moving from position 1 to position 2 is
View Solution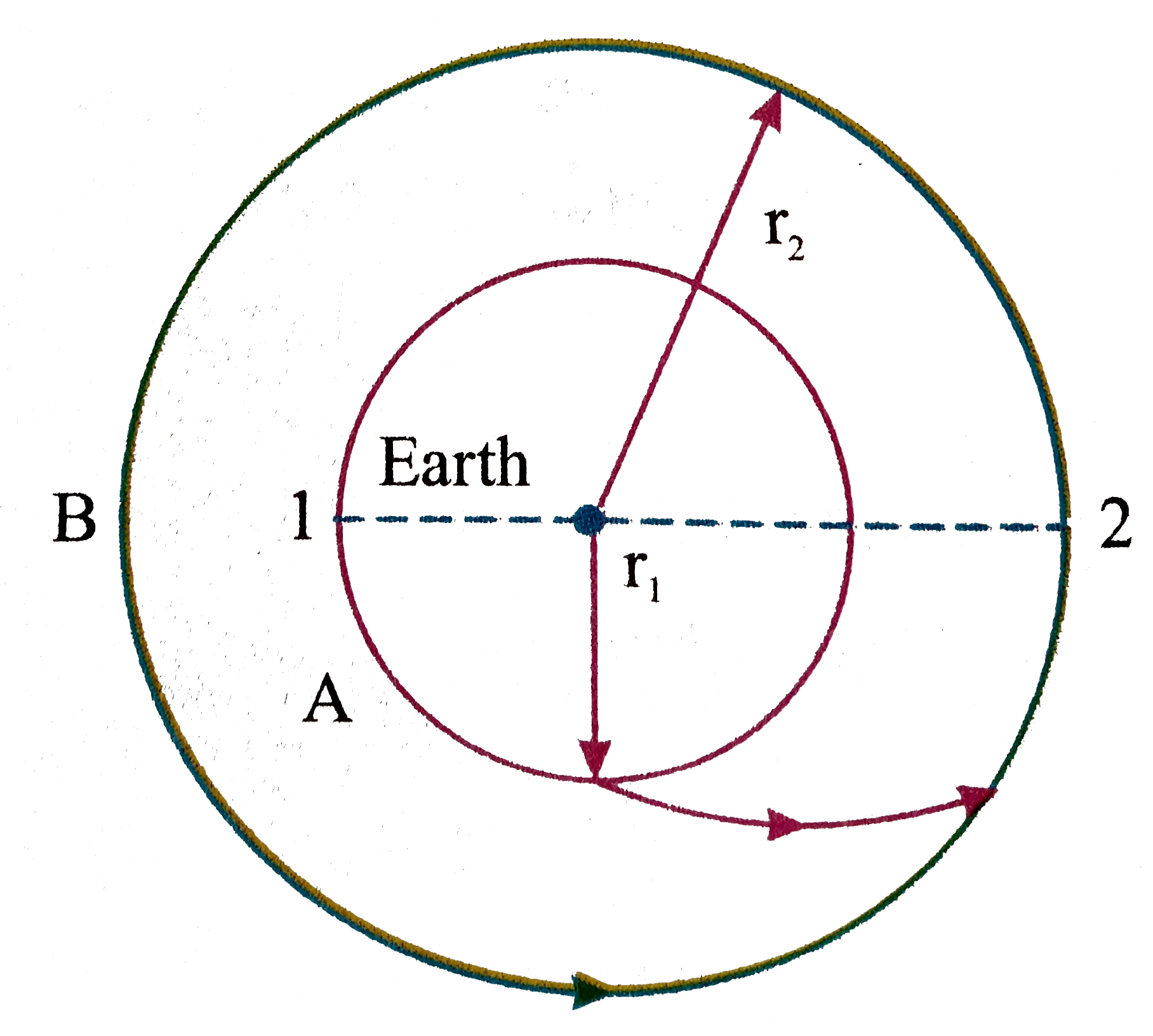
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If the two have same mass
View SolutionSuppose there are two planets, 1 and 2, having the same density but their radii are R1andR2 respectively, where R1>R2. The accelerations due to gravity on the surface of these planets are related as
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo racing cars having masse m1andm2 move in concentric circle of radii r1andr2 respectively. If their angular speed are same , then ratio of their linear speed is
View Solution
