If an oil drop of weight 3.2×10−13N is balanced in an electric field of 5×105Vm−1, find the charge on the oil drop.
The correct Answer is:0.64×10−18C
To solve the problem of finding the charge on the oil drop, we can follow these steps:
Step 1: Understand the Forces Acting on the Oil Drop
The oil drop is subjected to two main forces:
1. The gravitational force (weight) acting downwards, denoted as Fg.
2. The electrostatic force acting upwards due to the electric field, denoted as Fe.
Step 2: Set Up the Equation
Since the oil drop is balanced in the electric field, the upward electrostatic force equals the downward gravitational force:
Fe=Fg
Step 3: Write the Expressions for the Forces
The gravitational force can be expressed as:
Fg=mg
where m is the mass of the oil drop and g is the acceleration due to gravity.
The electrostatic force can be expressed as:
Fe=Q⋅E
where Q is the charge on the oil drop and E is the electric field strength.
Step 4: Substitute the Known Values
From the problem statement:
- The weight of the oil drop Fg=3.2×10−13N
- The electric field strength E=5×105V/m
Setting the forces equal gives:
Q⋅E=Fg
Step 5: Solve for the Charge Q
Rearranging the equation to solve for Q:
Q=FgE
Substituting the known values:
Q=3.2×10−13N5×105V/m
Step 6: Calculate the Charge
Now, perform the calculation:
Q=3.25×10−13×10−5=0.64×10−18C
Final Answer
Thus, the charge on the oil drop is:
Q=0.64×10−18C
---
The oil drop is subjected to two main forces:
1. The gravitational force (weight) acting downwards, denoted as Fg.
2. The electrostatic force acting upwards due to the electric field, denoted as Fe.
Since the oil drop is balanced in the electric field, the upward electrostatic force equals the downward gravitational force:
Fe=Fg
The gravitational force can be expressed as:
Fg=mg
where m is the mass of the oil drop and g is the acceleration due to gravity.
Fe=Q⋅E
where Q is the charge on the oil drop and E is the electric field strength.
From the problem statement:
- The weight of the oil drop Fg=3.2×10−13N
- The electric field strength E=5×105V/m
Q⋅E=Fg
Rearranging the equation to solve for Q:
Q=FgE
Q=3.2×10−13N5×105V/m
Now, perform the calculation:
Q=3.25×10−13×10−5=0.64×10−18C
Thus, the charge on the oil drop is:
Q=0.64×10−18C
Similar Questions
A beam of charged particle enters in a region of magnetic field of 5×10−3 weber m and electric field of 2.5×104Vm1,acting perpendicularly. Calculate the speed of particles perpendicular to electric and ,magnetic field , if their path remains unchanged. The given charge on particles and mass are 3.2×10−19C and 12×10−31 kg , respectively.
View SolutionAn oil drop of 12 excess electrons is held stationaty under a constant electric field of 2.55×104NC−1 in Millikan's oil drop experi,ment. The density of the oil is 1.26gcm−3. Estimate the radius of the drop. (g=9.81ms−2,e=1.60×1019C)
View Solution
Knowledge Check
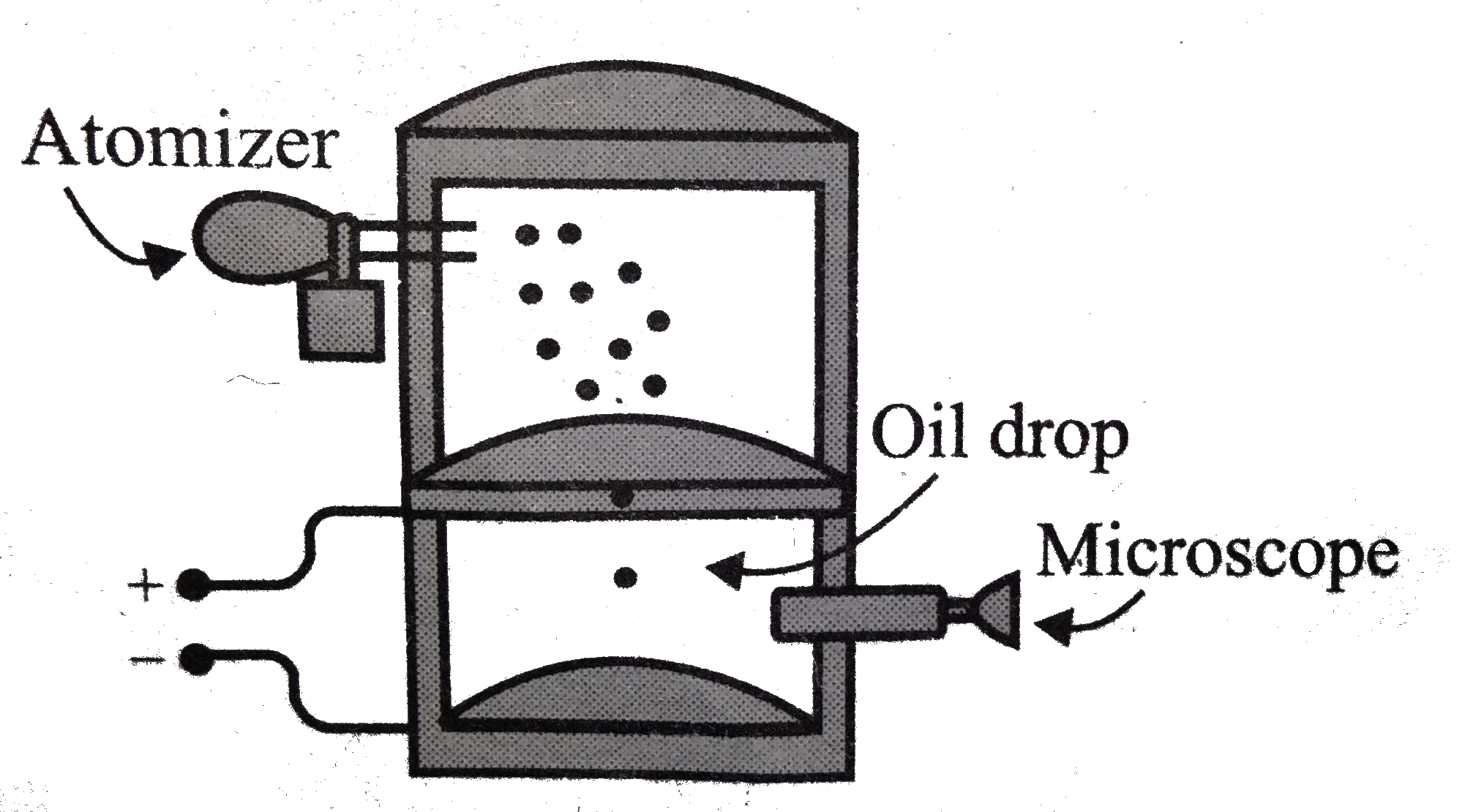
In 1909, Robert Millikan war the firest to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were pbserved with a magnitue eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of 1.6×10−19C− the charge of the electron. For this, he won the Nobel prize.
If a drop of mass 1.08×10−14kg remains stationary in an electric field of 1.68×105NC−1, then teh charge of this drop isA6.40×10−19CB3.2×10−19CC1.6×10−19CD4.8×10−19CIn Millikan's oil drop experiment, an oil drop mass 60×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop, assuming g=10m/s2 is
A6.2×10−11B16×10−9C16×10−11D16×10−13In Millikan's oil drop of mass 16×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop is: (assuming g=10m/s2)
A6.2×10−11B16×10−9C16×10−11D1.6×10−13
An oil drop of radius 2 mm with a density 3 g cm−3 is held stationary under a constant electric field 3.55×105Vm−1 in the Millikan's oil drop experiment. What is the number of excess electrons that the oil drop will possess ? Consider g=9.81m/s2
View SolutionA small particle of mass 1.8×10−30 kg and charge −3.5×10−19 C is dropped in a region of electric field of strength 2.8×105NC−1, directed in the upward direction. Calculate the time taken by the ball to cover a distance of 2 cm.
View SolutionFind the magnitude of force on a 10 μC charge placed in an electric field of 1×106N/C.
View SolutionIn Millikan's oil drop of mass 16×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop is: (assuming g=10m/s2)
View SolutionA particle of mass 6.4×10−27 kg and charge 3.2×10−19C is situated in a uniform electric field of 1.6×105Vm−1. The velocity of the particle at the end of 2×10−2m path when it starts from rest is :
View Solution

