A particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t1:t2:t3 is :
5:3:1
3:2:1
9:4:1
1:(√2−1):(√3:√2)
The correct Answer is:D
Step by step video, text & image solution for A particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t_(1):t_(2):t_(3) is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
Let A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View SolutionA particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View Solution
Knowledge Check
A particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal height h is.
At1:t2:t3=3:2:1Bt1:t2:t3=1:(√2−1):(√3−2)Ct1:t2:t3=1:√2:√3Dt1:t2:t3=1:(√2−1):(√3−√2)A particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal height h is.
At1:t2:t3=3:2:1Bt1:t2:t3=1:(√3−2)Ct1:t2:t3=√3:√2:1Dt1:t2:t3=1:(√2−1):(√3−√2)A body is released from the top of a tower of height h. It takes t sec to reach the ground. Where will be the ball after time t2 sec?
AAt h2 from the groundBAt h4 from the groundCdepends upon mass and volume of the bodyDat 3h4 from the ground
The balls are released from the top of a tower of height H at regular interval of time. When first ball reaches at the ground, the nth ball is to be just released and (n+12)th ball is at same distance 'h' from top of the tower. The value of h is
View SolutionA ball released from rest from the roof of a building of height 45 m at t = 0. Find the height of ball from ground at t = 2s.
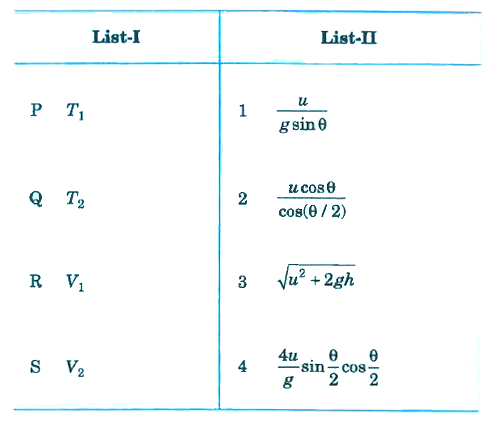
View SolutionA particle is projected from the top of a tower of height h with a speed u at an angle θ above the horizontal .
T1=Time taken by the projectile to reach the height of tower again .
T2=Time taken by the projectile to move at right angle to initial direction of motion .
V1=Speed of the projectile when it moves at an angle θ/2 with the horizontal .
V2=Speed with projectile strikes the ground .
.
View SolutionA small ball bearing is released at the top of a long vertical column of glycerine of height 2h. The bal bearing falls thorugh a height h in a time t1 and then the reamining height with the terminal velocity in time t2. Let W1 and W2 be the done against viscous drag over these height. Therefore,
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T/3 sccond?
View Solution
