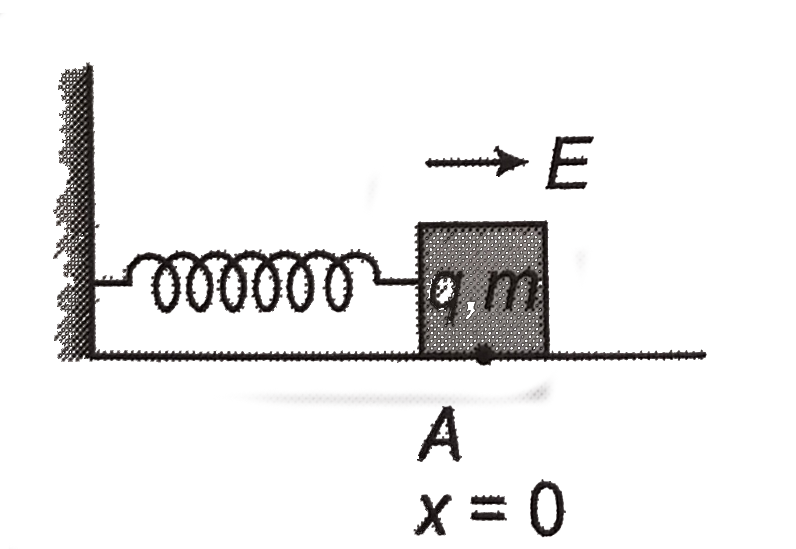
A block of mass m is attached to a spring of force constant k .Charges on the block is q. A horizontal electric field E is acting in the directions as shown.Block is released with the spring in unstretched position

(a) block will execute SHM
(b) time period of osciallation is 2π√mk
(c) amplitude of oscillation is qEk
(d) Block will oscillate but not simple harmonically
choose the correct answer
Block will execute SHM
Time period of oscillation is 2π√mk
Amplitude of oscillation is qEk
Block will oscillate but not simple harmonically.
The correct Answer is:A, B, C
Step by step video, text & image solution for A block of mass m is attached to a spring of force constant k .Charges on the block is q. A horizontal electric field E is acting in the directions as shown.Block is released with the spring in unstretched position (a) block will execute SHM (b) time period of osciallation is 2pisqrt(m)/(k) (c) amplitude of oscillation is (qE)/(k) (d) Block will oscillate but not simple harmonically choose the correct answer by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A block of mass m is attached to a spring of force constant k .Charges on the block is q. A horizontal electric field E is acting in the directions as shown.Block is released with the spring in unstretched position

block will execute SHM
(b) time period of osciallation is 2π√mk
(c) amplitude of oscillation is qEk
Block will oscillate but not simple harmonically
choose the correct answerAa and b are trueBd is trueCa,b,c are trueDa,b,c,d are true
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2kmA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionBlocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.

View Solution
