A cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the ratio of magnitude of torque on one side wall to the torque on base about the same axis
1:1
1:2
1:3
1:4
The correct Answer is:C
Step by step video, text & image solution for A cubical vessel (open from top) of side L is filled with a liquid of density rho. What is the ratio of magnitude of torque on one side wall to the torque on base about the same axis by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching
12 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
Similar Questions
A large vessel of height H is filled with a liquid of density ρ upto the brim. A small hole of radius r is made at the side vertical face, close to the base. The horizontal force is required to stop the gushing of liquid is
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View Solution
Knowledge Check
A cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the torque of hydrostatic force on a side wall about an axis passing through one of the bottom edges?AρgL44BρgL46C2ρgL43DρgL43A small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)
 AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3gA cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
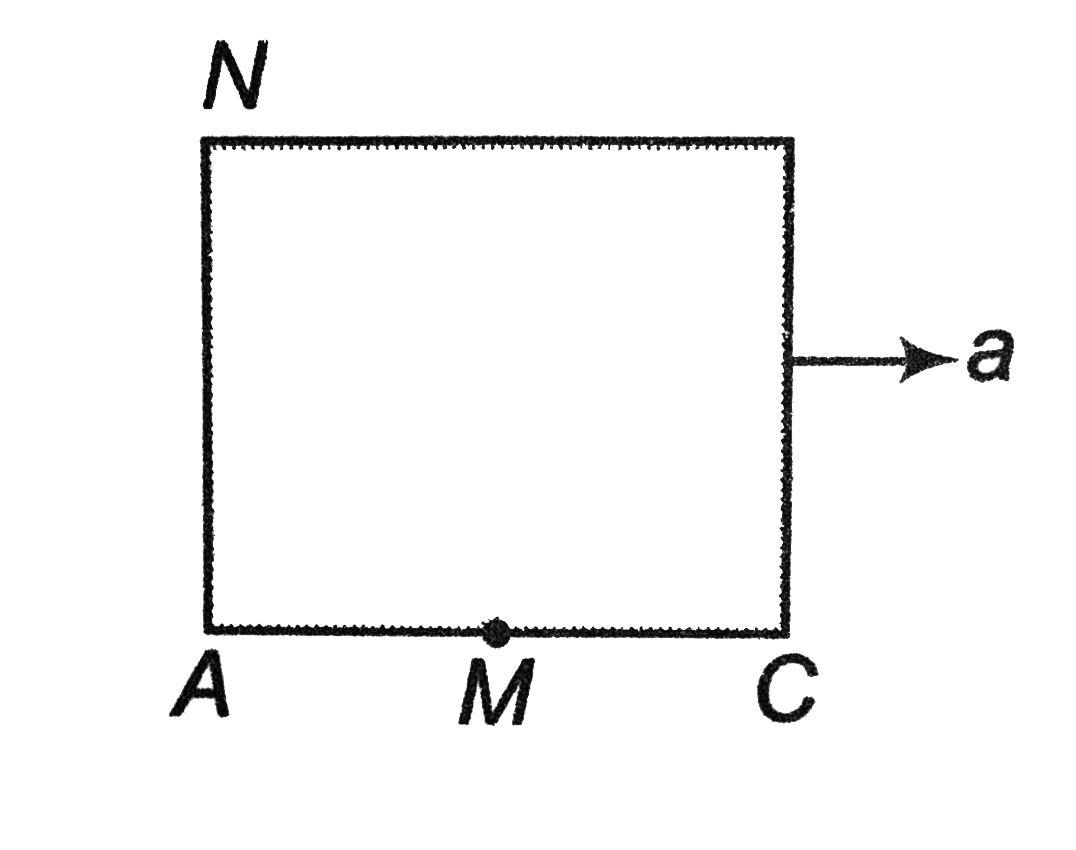 .AgB2gCg2Dzero
.AgB2gCg2Dzero
A small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
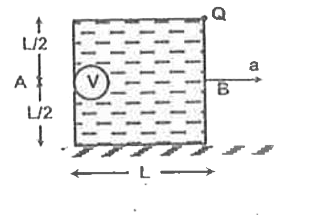
View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionThe following table has 3 comumn and 4 rows . . Based on table , there are Three questions . Each question has Four optios (A),(B) (C ) and (D) . ONLY One of these four options is correct .
A solid sphere of volume V and density ρS is tied by light inextensible string AB with the bottom surface of the vessel as shown in the figure . The vessel is filled with a liquid of density ρt .(given ρl>ρs)

Choose the correct combination in which tension in the string is maximum.
View Solution_S01_055_Q01.png)
A cuboid (a×a×2a) is filled with two immiscible liquid of density 2ρ&ρ as shown in the figure. Neglecting atmospheric pressure ratio of force on base & side wall of the cuboid is
(a). 2:3
(b). 1:3
(c). 5:6
(d). 6:5
View Solution
