In case i wedge B is stationary and block A starts sliding when the angle of plane is greater than a certain value θ. While in case ii wedge B is moving upwards with an accelration a0 and the block A starts sliding when the angle of plane is greater than α. Coeffiecient of friction between A and B in both the cases is same. then .
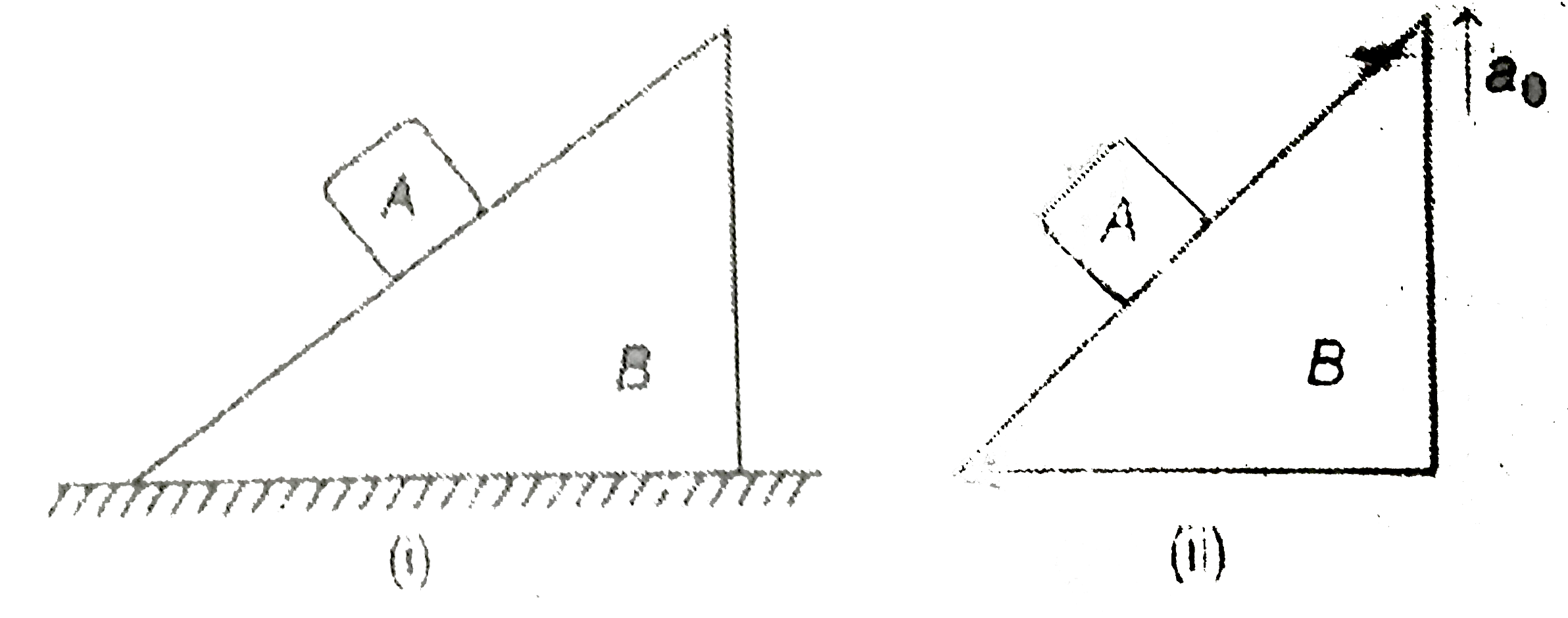
θ=α
θ>α
θ<α
tanθtanα=ga0
The correct Answer is:a
Step by step video, text & image solution for In case i wedge B is stationary and block A starts sliding when the angle of plane is greater than a certain value theta. While in case ii wedge B is moving upwards with an accelration a_(0) and the block A starts sliding when the angle of plane is greater than alpha. Coeffiecient of friction between A and B in both the cases is same. then . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
View SolutionProve that the horizontal range id same when angle of projection is (i) greater than 45∘ by certain value and (ii) less than 45∘ by the same value.
View Solution
Knowledge Check
A block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
AsinθBcosθCtanθDIndependent of θA block is at rest on an inclined plane making an angle α with the horizontal . As the angle α of the incline is increased the block starts slipping when the angle of inclination becomes θ. The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle θ to the horizontal. Then the coefficient of friction is equal to
AsinθBcosθCtanθDIndependent of θA block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.
If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :AincreasesBdecreasesCremain sameDincrease of a>g
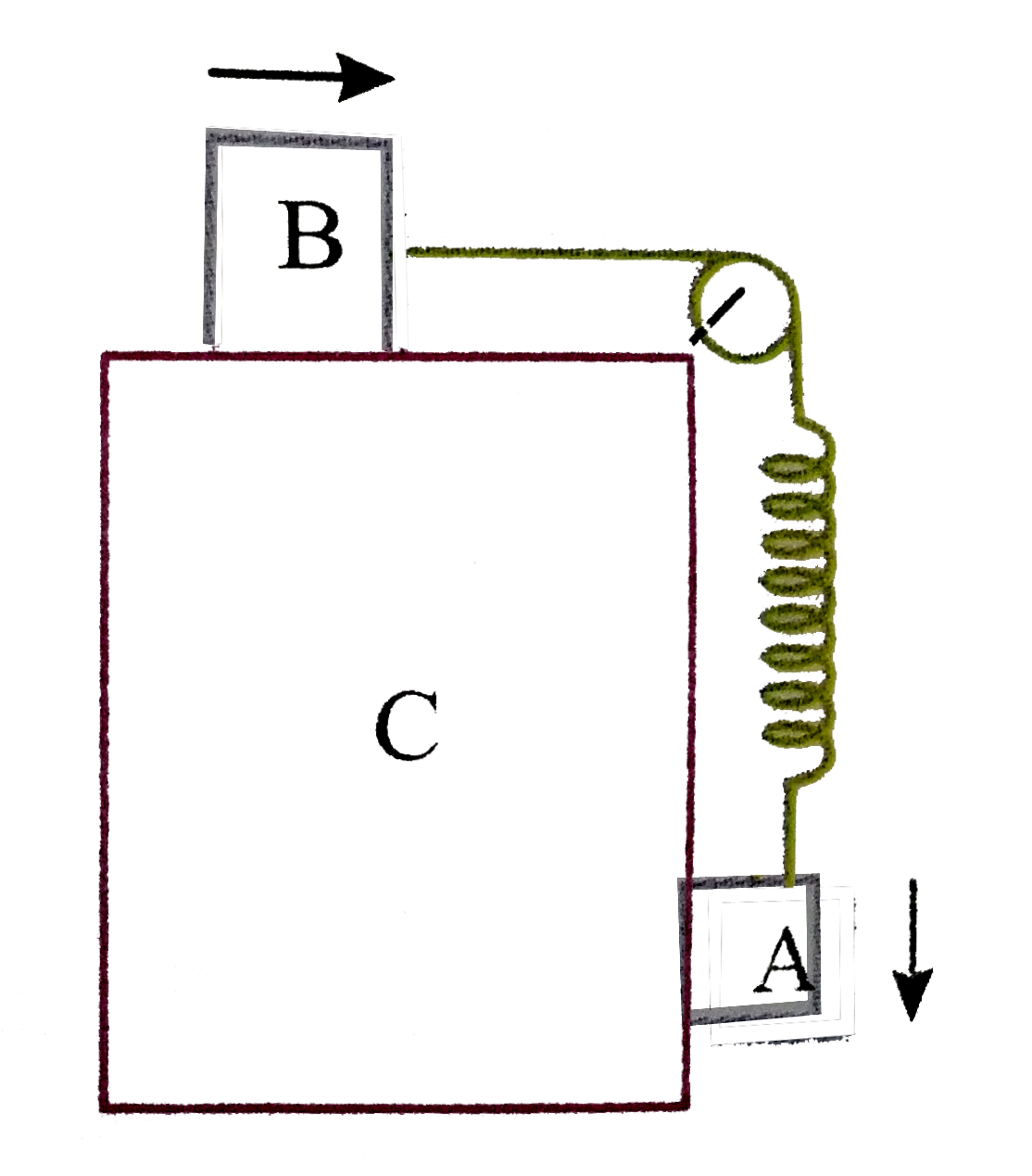
Two blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in Block B slides over the horizontal surface of a stationary block C and the block. A slides along the vertical side of C, both with same uniform speed. The coefficient of friction between the surface of the blocks is 0.2 Force constant of the spring is 1960 N/m if the mass of block A is 2 kg calculate the mass of the block B and the energy stored in the spring.
View SolutionTwo blocks A and B are connected to each other by a string and a spring , the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surface and blocks is 0.5K=2000N/m. If mass of A is 2kg calculate mass of B.
.
View Solution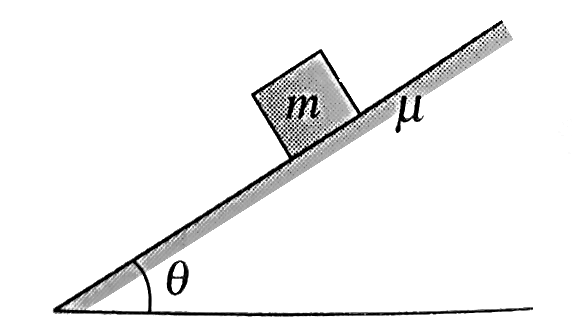
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View Solution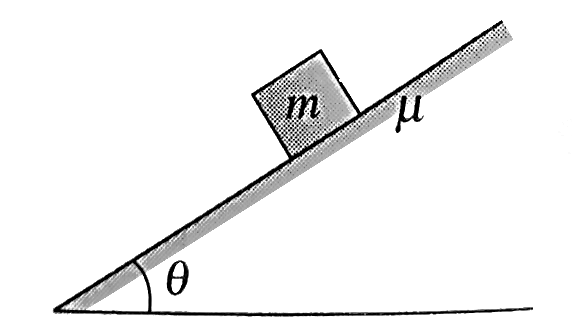
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
View Solution