An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
25mR2
mr22
mR2
32mR2
The correct Answer is:B
When the body rolls, it has both translational and rotational Kinetic energies.
Translational K.E. =12mv2
and Rotational K.E. =12Iω2=12Iv2R2
∴ Total energy at A=EA=12mv2+12Iv2R2
=12v2(m+1R2)
AT B it has only P.E. = mgh
=mg.3v24g=3mv24=EB
By the principle of conservation of energy
EA=EB∴12v2m+(IR2)=34mv2
∴m+IR2=32m∴I=mR22
This is the M.I. of a disc. ∴ The body is a disc
Topper's Solved these Questions
Similar Questions
A body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View Solution
Knowledge Check
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
Asolid sphereBhollow sphereCdiscDringA body of mass M and radius R is rolling horizontally without slipping with speed v . It then rolls up a hill to a maximum height h . If h=5v26g , what is the M.I of the body ?
AMR22B23MR2C34Mr2D25MR2A mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
Athe body is identified to be a disc or a solid cylinderBthe body is a solid sphereCmoment of inertia of the body about instantaneous axis of rotation is 32mr2Dmoment of inertial of the body about instantaneous axis of rotation is 75mr2
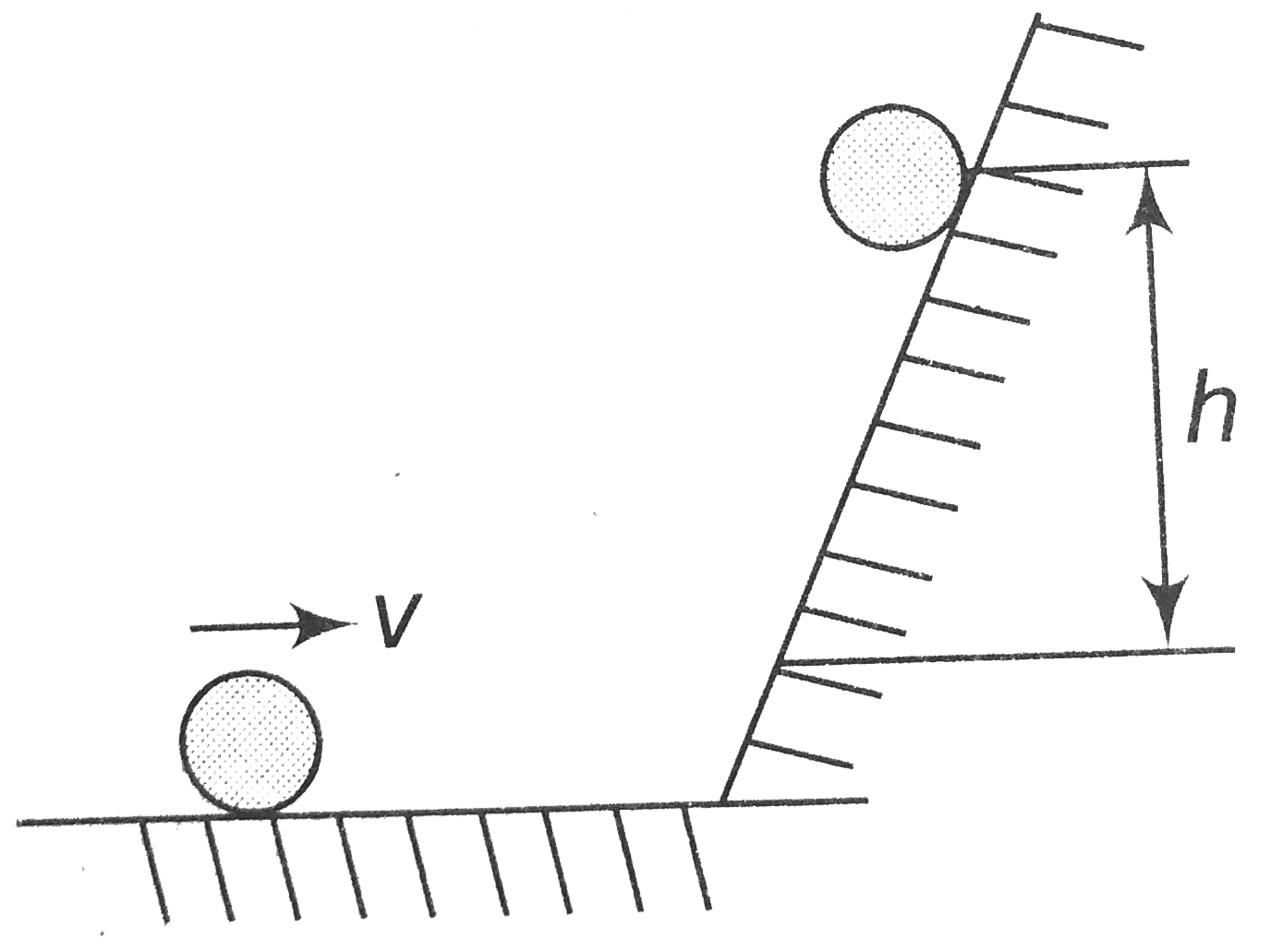
A disc of radius R and mass M is rolling horizontally without slipping with speed with speed v. It then moves up an incline as shown in figure. The maximum height upto which it can reach is.
 .
.
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with the speed u . Now if it rolls up vertically , the maximum height it would attain will be
View SolutionA loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity 'v' . It reaches upto a maximum height of 3v24g with respect to the initial position . The object is
View Solution
