Moment of inertia of a ring of mass m = 3 gm and radius r = 1 cm about an axis passing through its edge and parallel to its natural axis is
10 gram cm2
100 gram cm2
6 gram cm2
1 gram cm2
The correct Answer is:C
I=mr2+mr2=2mr2=6 gram - cm2
Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View Solution
Knowledge Check
The moment of inertia of a ring of mass 5 gram and radius 1 cm about and axis passing through its edge and parallel to its natural axis is
A5g−cm2B2.5 g - cm2C20 g - cm2D10 g - cm2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter?
AIBI2CI√2DI+MR2
What is the moment of inertia of a ring of mass 2kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane ? Also find the moment of inertia about a parallel axis through its edge.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
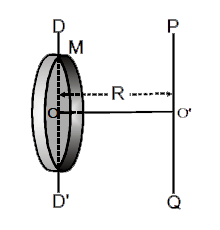
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter ?
View SolutionMoment of inertia of a hollow cylinder of mass M and radius r about its own axis is
View Solution
